2.2. Размерность и базис линейного пространства

Элементы называются Линейно независимыми, если из равенства следует, что В противном случае элементы Линейно зависимы.

Если в линейном пространстве найдено линейно независимых элементов, а любые уже линейно зависимы, то число называется Размерностью пространства и обозначается , т. е. .

Совокупность элементов из называется Базисом линейного пространства , если любой элемент единственным образом представим в виде Числа называются Координатами элемента в базисе

Пример 5. Пусть – линейное пространство, элементами которого являются квадратные матрицы 2-го порядка.

Тогда матрицы образуют базис в . Так, если то т. е. в базисе координатами элемента являются

Пример 6. Рассмотрим линейное -мерное пространство, элементами которого являются упорядоченные наборы вещественных чисел

Которые мы будем называть Векторами, а числа – их Координатами в некотором заданном базисе. Если рассмотренное линейное пространство вещественно, то оно называется Арифметическим векторным пространством и обозначается . Очевидно, векторы …, Образуют базис в .

Для каждого можно составить матрицу-столбец размера

,

Которую будем называть Вектор-столбец. Такие векторы-столбцы образуют линейное пространство, которое также называется арифметическим векторным пространством. Ортонормированный базис в нём образуют векторы-столбцы

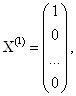
Объектом дальнейших наших исследований будут арифметические векторные пространства .

< Предыдущая		Следующая >