1.4. Решение СЛАУ с помощью блочных матриц

Рассмотрим систему линейных алгебраических уравнений (СЛАУ) вида

Запишем эту систему в матричной форме: , где , . Выберем число и разобьём матрицы и на блоки таким образом:

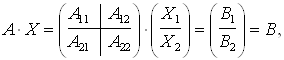
Где , т. е. матрицы и – квадратные. Решим систему матричных уравнений:

Пусть – квадратная матрица порядка – невырожденная. Умножая второе уравнение системы слева на , получим: Так как , то . Подставляя найденное выражение для в первое уравнение системы, получим:

,

Откуда

Если известна , то из последнего равенства легко найти

Замечание 1. Этот метод особенно удобен, если нужно найти первые неизвестных СЛАУ.

Замечание 2. Существует алгоритм, позволяющий находить после разбиения матрицы на блоки.

Пример 3. Найти , решая СЛАУ с помощью блочных матриц:

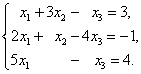
Решение. Выполним разбиение матриц и системы на блоки следующим образом :

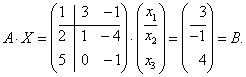
Уравнение для нахождения имеет вид:

Так как 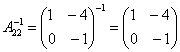, то:

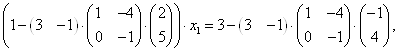
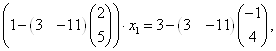
Ответ: .

Литература: [2, 3, 4, 7, 15].

< Предыдущая		Следующая >