1.3. Блочные матрицы
Матрица, имеющая более чем одну строку или столбец, прямыми, проведенными между строками и (или) столбцами, может быть разбита на блоки – подматрицы. Полученная таким образом матрица называется Блочной.
Например, матрица ![]() может быть разбита на блоки следующим образом:
может быть разбита на блоки следующим образом:

Обозначим 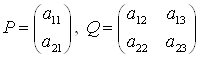 ,
, ![]() В этих обозначениях матрица
В этих обозначениях матрица ![]() примет вид:
примет вид: 
Любую матрицу, имеющую более чем одну строку или столбец, можно представить, и при этом не единственным образом, в блочной форме. Переход к такому виду матрицы иногда бывает полезным, так как сводит вычисления с матрицами больших размеров к вычислениям с матрицами меньших размеров.
Блочные матрицы одинакового размера и одинакового разбиения на блоки называются Конформными.
Операции над конформными матрицами целесообразно проводить над блоками матриц по правилам, приведенным в п.1.1.
Действия над блочными матрицами
1. Сложение.
Пусть ![]() и
и ![]() – конформные матрицы:
– конформные матрицы:

Тогда их сумма:  .
.
2. Умножение на число 
3. Умножение блочных матриц.
Выполнение условия согласованности в операции умножения для блочных матриц предполагает, что, если:
 То
То  .
.
Предположим, что все блоки ![]() и
и ![]() таковы, что число столбцов блока
таковы, что число столбцов блока ![]() совпадает с числом строк блока
совпадает с числом строк блока ![]() . В частности, например, все блоки матриц
. В частности, например, все блоки матриц ![]() и
и ![]() квадратные одного порядка. Тогда произведением матриц
квадратные одного порядка. Тогда произведением матриц ![]() и
и ![]() называется матрица
называется матрица
 ,
,
Где ![]()
Пример 1. Найти ![]() , если
, если ![]() ,
,  .
.
Решение. Введём обозначения: ![]() где
где ![]()
![]() , а
, а 
Поскольку правило согласованности умножения матриц выполняется, то
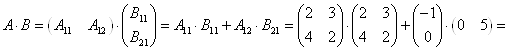
![]()
Ответ: ![]() .
.
Пример 2. Найти ![]() , если
, если  ,
, 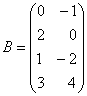 .
.
Решение. Представим матрицы ![]() и
и ![]() в следующем виде:
в следующем виде:
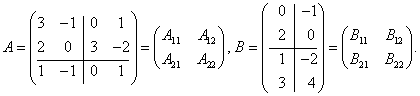
Обозначим 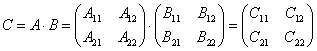 , тогда
, тогда

![]()
![]()
Таким образом,  .
.
Ответ: 
Замечание. Безусловно, выполнить умножение матриц ![]() и
и ![]() в Примерах 1 и 2 можно и не представляя их в блочной форме. Примеры приведены для иллюстрации применения к умножению матриц метода разбиения их на блоки.
в Примерах 1 и 2 можно и не представляя их в блочной форме. Примеры приведены для иллюстрации применения к умножению матриц метода разбиения их на блоки.
Блочная матрица  где
где ![]() – квадратные матрицы, в общем случае различных порядков, а остальные блоки – нулевые матрицы, называется Квазидиагональной.
– квадратные матрицы, в общем случае различных порядков, а остальные блоки – нулевые матрицы, называется Квазидиагональной.
Можно доказать, что
1) ![]()
2) ![]()
Рассмотрим две квазидиагональные матрицы:


Где каждая пара![]() и
и ![]()
![]() – квадратные матрицы одного порядка. Тогда их сумма и произведение определяются следующим образом:
– квадратные матрицы одного порядка. Тогда их сумма и произведение определяются следующим образом:


Из правила произведения блочных матриц следует, что

Если ![]() – невырожденная матрица, то эта формула имеет место для любого целого
– невырожденная матрица, то эта формула имеет место для любого целого ![]() .
.
| < Предыдущая | Следующая > |
|---|