1.2. Элементарные преобразования матриц

К элементарным преобразованиям матриц относятся:

1) перестановка строк (столбцов) матрицы;

2) умножение строки (столбца) матрицы на произвольное число, отличное от нуля;

3) умножение строки (столбца) матрицы на произвольное число и добавление её к другой строке (столбцу).

Пусть – произвольная квадратная матрица порядка . Выясним, каким элементарным преобразованиям матрицы соответствует умножение её слева или справа на матрицу , полученную из единичной матрицы порядка следующими способами.

Задача 1. Матрица получена из единичной матрицы -го порядка заменой 1 в -й строке на число .

Решение. Пусть :

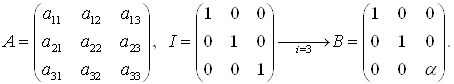Тогда:

Задача 2. Матрица получена из единичной матрицы -го порядка заменой некоторого элемента на 1.

Решение. Пусть : . Тогда:

1) , т. е. -й столбец заменяется на сумму -го и -го столбцов;

2) т. е. -я строка заменяется на сумму -й и -й строк.

Задача 3. Матрица – матрица получена из матрицы перестановкой двух её строк или столбцов.

Решение. Пусть : 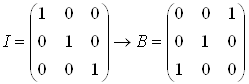. Тогда

Ранг матрицы равен максимальному числу линейно независимых строк или столбцов этой матрицы.

Если квадратная матрица порядка невырожденная, то .

Сумма диагональных элементов квадратной матрицы порядка называется её Следом и обозначается . Таким образом, .

Очевидно,

Для двух квадратных матриц одного порядка

< Предыдущая		Следующая >