44. Положительно определённые квадратичные формы

Определение 65. Действительная квадратичная форма называется Положительно определённой, если для любого вектора А ¹ 0 имеет место J(А) > 0.

Теорема 68. Действительная квадратичная форма является положительно определённой тогда и только тогда, когда её ранг и положительный индекс инерции равны числу неизвестных.

Доказательство. Þ Пусть J(А) – действительная положительно определённая квадратичная форма. Пусть она приводится к нормальному виду

У12 + У22 + … + Ук2 – Ук+12 – … – Уr2 (*),

В котором либо R < n, либо R = n, но К < n. Пусть преобразование координат, с помощью которого форма приведена к нормальному виду, задаётся формулами Уі = (**). Определитель этих формул отличен от нуля. Если R < n, То возьмём У1 = у2 = … = уn–1 = 0, Уn = 1 и подставим в (**). Получим систему N линейных неоднородных уравнений с N Неизвестными и с определителем, отличным от нуля. По правилу Крамера эта система имеет единственное решение. Очевидно, это решение не нулевое, поэтому определяет ненулевой вектор А. Но тогда J(А) = 0, что противоречит определению положительно определённой формы. Аналогично приходим к противоречию и в случае R = n, но К < n. Итак, если форма положительно определённая, то её нормальный вид У12 + У22 + … + Уn2. Это и значит, что ранг и положительный индекс инерции равны N.

Ü Ранг и положительный индекс инерции действительной квадратичной формы равны N. Докажите самостоятельно, что форма положительно определённая.

Отметим без доказательства ещё одну теорему о положительно определённых действительных квадратичных формах.

Теорема 69. Действительная квадратичная форма является положительно определённой тогда и только тогда, когда все главные миноры её матрицы положительны.

Теорема 70. Квадрат длины вектора в любом базисе евклидова пространства задаётся положительно определённой квадратичной формой.

Доказательство. Пусть ЕN – N-мерное евклидово пространство, Е = (Е1, Е2, … , Еn) – базис в нём и Г – матрица Грама, задающая скалярное произведение векторов в этом базисе. Если А = Х1Е1 + Х2Е2 + … + ХnЕn , В = У1Е1+ У2Е2 + … + УnЕn, то (А, в) = Х Т×Г×У, где Х Т– строка координат вектора А, У – Столбец координат вектора В. Следовательно, А2 = (А, А) = Х Т×Г×Х. Если сравнить с формулой (60), то получим, что Х Т×Г×Х есть квадратичная форма с матрицей Г. В пространстве ЕN есть ортонормированный базис. В этом базисе А2 = Х12 + Х22 +…+ ХN2. Но это значит, что при переходе к ортонормированному базису квадратичная форма Х Т×Г×Х Приводится к нормальному виду Х12 + Х22 +…+ ХN2. По теореме 68 получаем, что форма Х Т×Г×Х является положительно определённой.

Пример. Какие из следующих квадратичных форм являются положительно определёнными?

1. 4Х12 – Х1х2 + 3Х22 – Х2х3 + 6Х2х4.

2. 4Х1х2 – Х1х3 + 2Х22 – 4Х2х3 + 3Х2х4 + 5Х42.

3. 4Х12 – 5Х1х2 + 3Х22 – 2Х2х3 + Х32 + 4Х2х4 – Х42 .

Решение. Ответить на вопрос можно двумя способами: привести форму к каноническому виду или вычислить главные миноры матрицы данной формы. Для первой формы используем первый способ, для второй и третьей – второй способ.

1. 4Х12 – Х1х2 + 3Х22 – Х2х3 + 6Х2х4 = (4Х12 – Х1х2 + ) – + 3Х22 – Х2х3 + 6Х2х4 =

= (2Х1–)2 + ( х22 –

= (2Х1–)2 + (– =

= (2Х1–)2 + (– . Отсюда следует, что ранг данной формы равен 3, т. е. меньше числа переменных, поэтому эта форма не является положительно определённой (теорема 68).

2. Составим матрицу второй квадратичной формы и найдём главные её миноры.

А = 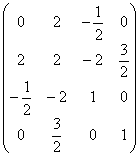, М1 = 0. Уже отсюда следует, что форма не является положительно определённой (теорема 69).

3. Составим матрицу третьей квадратичной формы и найдём главные её миноры.

А = , М1 = 4 > 0, М2 = 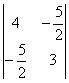= 5,75 > 0, М3 = 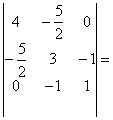1,25 > 0,

М4 = ½А½= 14,25 > 0. Итак, все главные миноры положительны. Следовательно, третья квадратичная форма положительно определённая.

< Предыдущая		Следующая >