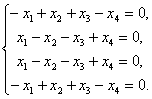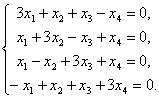39. Самосопряженные (симметрические) линейные преобразования
Определение 56. Линейное преобразование называется Самосопряжённым, если оно совпадает со своим сопряжённым преобразованием ( J - самосопряжённое Û J = J*).
Из формулы (52) следует, что линейное преобразование J Евклидова пространства будет самосопряжённым тогда и только тогда, когда (А, J(В)) = (J(А), В) (55).
Пусть в ЕN зафиксирован базис Е = (Е1, Е2, ... , Еn), Г – матрица Грама и А – матрица самосопряжённого преобразования J . В этом случае А* = А и формула (53) будет иметь вид: А = Г–1×АТ×Г . Если базис ортонормированный, то А = АТ, т. е. матрица А – симметрическая. Итак, верна
Теорема 56. Линейное преобразование является самосопряжённым тогда и только тогда, когда в ортонормированном базисе оно задаётся симметрической матрицей.
Теорема 56 объясняет тот факт, что самосопряжённое преобразование называют также Симметрическим.
Отметим некоторые свойства симметрических преобразований.
10. Тождественное преобразование является симметрическим.
Действительно, тождественное преобразование в любом базисе задается единичной матрицей. Но единичная матрица – симметрическая.
20. Сумма симметрических преобразований есть преобразование симметрическое.
Это утверждение следует из того, что сумма двух симметрических матриц есть матрица симметрическая.
30. Произведение симметрического преобразования на действительное число есть симметрическое преобразование.
Действительно, если симметрическую матрицу умножить на действительное число, то получится симметрическая матрица.
40. Если симметрическое преобразование J Имеет обратное преобразование J–1, то J–1 – симметрическое преобразование.
Это свойство тоже следует из свойств симметрических матриц.
50. Если линейные преобразования J И Y Евклидова пространства симметрические, то их произведение будет симметрическим преобразованием тогда и только тогда, когда они перестановочны, т. е. J×Y = Y×J.
Действительно, для симметрических преобразований J И Y Имеем (J×Y)* = Y*×J* = YJ.
J×Y Будет симметрическим тогда и только тогда (по определению), когда (J×Y)* = J×Y . отсюда следует, что J×Y Будет симметрическим тогда и только тогда, когда J×Y = YJ.
60. Пусть J Симметрическое преобразование евклидова пространства Е. Если Н – инвариантное подпространство преобразования J, то и ортогональное дополнение Н^ является инвариантным подпространством преобразования J.
Это свойство следует из соответствующего свойства преобразования J*.
Теорема 57. Все корни характеристического многочлена симметрического преобразования действительные.
Доказательство. Пусть в пространстве Еn зафиксирован ортонормированный базис Е, пусть J симметрическое преобразование и А – его матрица в базисе Е. Матрица А – симметрическая. Пусть L0 – произвольный корень характеристического многочлена |А – LЕ |. Однородная система уравнений (А –L0Е )×Х = 0 имеет ненулевые решения, ибо определитель её равен нулю. Эти решения могут быть и комплексные. Пусть Х = (Х1, х2, …, хn )Т – одно из таких решений. Тогда Ах = L0х. Умножим обе части этого матичного уравнения на строку ![]() Т , получим
Т , получим ![]() Т×А×х =L0×
Т×А×х =L0×![]() Т×х (*). Вычисляя
Т×х (*). Вычисляя ![]() Т×х, получим
Т×х, получим ![]() Т×х =
Т×х = ![]() . Отсюда следует, что
. Отсюда следует, что ![]() Т×х действительное число, не равное нулю. Покажем, что, если матрица А Симметрическая, то число
Т×х действительное число, не равное нулю. Покажем, что, если матрица А Симметрическая, то число ![]() Т×А×х тоже действительное. Число
Т×А×х тоже действительное. Число ![]() Т×А×х можно рассматривать как квадратную матрицу первого порядка. Такая матрица не меняется при транспонировании, т. е.
Т×А×х можно рассматривать как квадратную матрицу первого порядка. Такая матрица не меняется при транспонировании, т. е. ![]() Т×А×х = (
Т×А×х = (![]() Т×А×х)Т = ХТ×АТ×
Т×А×х)Т = ХТ×АТ×![]() = ХТ×А×
= ХТ×А×![]() . Кроме того
. Кроме того ![]() . В двух последних равенствах правые части одинаковы, следовательно, равны и левые части, т. е.
. В двух последних равенствах правые части одинаковы, следовательно, равны и левые части, т. е. ![]() Т×А×х =
Т×А×х = ![]() . Следовательно, число
. Следовательно, число ![]() Т×А×х Действительное. Из равенства (*) следует, что L0 – действительное число.
Т×А×х Действительное. Из равенства (*) следует, что L0 – действительное число.
Следствие 1. Все характеристические корни симметрической матрицы А являются действительными.
Следствие 2. Симметрическое преобразование евклидова пространства имеет собственные векторы.
Теорема 58. Собственные векторы симметрического преобразования, принадлежащие различным собственным значениям, ортогональны.
Доказательство. Пусть J – симметрическое преобразование евклидова пространства Еn, L1, L2, = его собственные значения и L1 ¹ L2 . Пусть А И В – собственные векторы, принадлежащие собственным значениям L1 И L2 Соответственно. Тогда J(А) = L1А, J(В) = L2В. По определению симметрического преобразования (А, J(В)) = (J(А), В). Отсюда (А, L2В) = (L1А, В), L2(А, В) = L1(А, В), (L1 – L2)×(А, В) = 0. Так как L1 ¹ L2 , то (А, В) = 0. Так как собственные векторы не нулевые, то А ^ В.
Теорема 59. Линейное преобразование J: Еn ® Еn является симметрическим тогда и только тогда, когда в Еn существует ортонормированный базис, состоящий из собственных векторов преобразования J.
Доказательство. Ü Пусть Е = (Е1, Е2, ..., Еn) – ортонормированный базис, состоящий из собственных векторов преобразования J. В этом случае J(Ек) = LкEk для любого К = 1, 2, …, N. Следовательно, в данном базисе преобразование J имеет диагональную, а поэтому и симметрическую матрицу, т. е. J – симметрическое преобразование.
Þ Пусть линейное преобразование J: Еn ® Еn симметрическое. Доказательство проведём методом математической индукции. При N = 1 каждый вектор отображается на пропорциональный ему вектор, т. е каждый вектор является собственным. Поэтому есть базис из собственных векторов.
Предположим, что утверждение теоремы верно для евклидова пространства размерности (N – 1). Пусть Еn – евклидово пространство размерности N. По следствию 2 теоремы 54 J имеет собственные векторы. Пусть Е1 – собственный вектор, принадлежащий собственному значению L1. Можно считать, что этот вектор единичный, иначе его можно нормировать. Пусть Е1 = <Е1>. Очевидно, J (Е1) = Е1. Ортогональное дополнение Е1Т тоже будет инвариантным относительно J. Так как dim Е1Т = N – 1, то в Е1Т существует ортонормированный базис, состоящий из собственных векторов преобразования J. Пусть это ( Е2, ..., Еn). Но тогда (Е1, Е2, ..., Еn) – ортонормированный базис из собственных векторов в пространстве Еn .
Из доказанной теоремы вытекает следующее утверждение.
Теорема 60. Любая симметрическая матрица А Приводится к диагональному виду с помощью ортогональной матрицы.
Доказательство. Пусть А – симметрическая матрица. Её можно рассматривать как матрицу некоторого симметрического преобразования J В ортонормированном базисе Е = (Е1, Е2, ..., Еn) пространства Еn . По теореме 56 в Еn существует ортонормированный базис Е1 = (Е11, Е21, ..., Еn1), состоящий из собственных векторов преобразования J. Если А1 – матрица j в базисе Е1, то А1 – Диагональная. Пусть Т – матрица перехода от базиса Е к базису Е1. Тогда Т – ортогональная и А1 = Т–1×А×Т.
Пример. Привести к диагональному виду матрицу
|
А = |
Решение. Характеристический многочлен матрицы А
|
Имеет корни L1 = L2 = L3 = 1, L4 = – 3. Все они являются собственными значениями матрицы А. Найдём соответствующие собственные векторы.
При L = 1 получаем систему уравнений
|
|
Ранг этой системы равен 1, поэтому фундаментальная системы состоит из 3-х решений, например, А1 = (1, 1, 0, 0), А2 = (1, 0, 1, 0), А3 = ( –1, 0, 0, 1). Полученную систему векторов нужно ортонормировать. Для этого нужно задать матрицу Грама. Так как скалярное произведение любое, то зададим Г = Е. Тогда получим |
Следующую ортонормированную систему:
Е11 = ![]() Е21 =
Е21 = ![]() , Е31 =
, Е31 = ![]() .
.
При L = –3 получаем систему уравнений
|
|
Ранг этой системы равен 3, поэтому фундаментальная системы состоит из 1-го решения, например, А4 = (1, –1, –1, 1). Нормируя его, получим Е41 = Система векторов Е11, Е21, Е31, Е41 – ортонормированный базис из |
Собственных векторов. Матрица перехода от исходного базиса к базису Е1 будет
|
Т = |
Т–1 = |
А = ТА1Т–1 =  ×
× 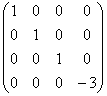 ×
× 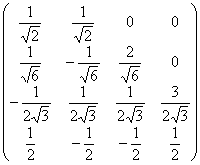 .
.
.
Теорема 62. Для любого линейного преобразования J: Еn ® Еn преобразования J*J И Jj* являются неотрицательными, т. е. эти преобразования симметрические, а все их собственные значения – неотрицательные числа.
Доказательство. (J*J)* = J*(J*)* = J*J. Следовательно, J*J – симметрическое преобразование. Пусть L – собственное значение преобразования J*J и А – соответствующий собственный вектор. Тогда ((J*J)(А), А) = (J*(J(А),А) = (J(А), J(А)) = =½J(А)½2. С другой стороны, ((J*J)(А), А) = (LА, А) = L½А½2. Следовательно, ½J(А)½2 = L½А½2. Так как А ¹ 0, то L ³ 0. Для преобразования Jj* рассуждения аналогичны.
Определение 57. Симметрическое линейное преобразование называется Положительно определённым, если для любого ненулевого вектора А выполняется неравенство (А, J(А)) > 0.
Теорема 61. Симметрическое преобразование является положительно определённым тогда и только тогда, когда все его собственные значения положительные.
Доказательство. Þ Пусть симметрическое преобразование J Является положительно определённым. Тогда (А, J(А)) > 0 для любого вектора, в частности для любого собственного вектора. Но если А – собственный вектор, то J(А) = LА. Следовательно, 0 < (А, LА) = L(А, а). Так как для ненулевого вектора (А, а) > 0, то L > 0.
Ü Пусть все собственные значения симметрического преобразования J положительные. Выберем в пространстве Еn базис Е = (Е1, Е2, ... , Еn), состоящий из собственных векторов этого преобразования. Если А = Х1Е1 + Х2Е2 + … + ХnЕn , то (А, J(А)) = (![]() =
= ![]() . Если А ¹ 0, то (А, J(А)) > 0, т. е. преобразование J положительно определённое.
. Если А ¹ 0, то (А, J(А)) > 0, т. е. преобразование J положительно определённое.
Замечание. Симметрическое линейное преобразование называется Неотрицательным, если для любого ненулевого вектора А выполняется неравенство (А, J(А)) ³ 0.
Симметрическое линейное преобразование называется Отрицательно определённым, если для любого ненулевого вектора А выполняется неравенство (А, J(А)) < 0любого вектора А получим (А, J*J(А)) = (J(А), J(А)) ³ 0. Следовательно, преобразование J*J неотрицательное.
| < Предыдущая | Следующая > |
|---|
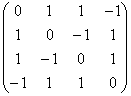 .
.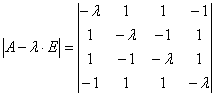 = (L – 1)3×(L + 3)
= (L – 1)3×(L + 3)