37. Ортогональные линейные преобразования

Определение 53. Линейное преобразование J Евклидова пространства Е называется Ортогональным, если для любых векторов А и В из Е выполняется условие

(А, в) = (J(А), J(В)) (49)

Свойства ортогональных преобразований.

Пусть J – ортогональное преобразование пространства Е.

10. | А| = |J(А)| для любого вектора А.

| А| = = = | J(А)|.

20. = Для любых векторов А И .

30. Пусть Еn конечномерное евклидово пространство, е = (Е1, Е2, ... , Еn) – базис в нём, А – матрица преобразования J и Г – Матрица Грама в этом базисе. Тогда J(А) = А×х, J() = А×у, Где Х И У –Столбцы координат векторов А И соответственно; (А, ) = ХТ×Г×у, (J(А), J()) = (А×х)Т×Г×( А×у) = ХТ×(АТ×Г×А)×У. Так как (А, ) = (J(А), J()), то Г = АТ×Г×А. Итак, матрица ортогонального преобразования удовлетворяет условию

Г = АТ×Г×А (50)

Справедливо и обратное. Если в Еn зафиксирован базис и Г – матрица Грама в этом базисе, то матрица А, удовлетворяющая условию (50), задаёт ортогональное преобразование.

Если базис Е = (Е1, Е2, ... , Еn) ортонормированный, то Г = Е и формула (50) примет вид

АТ× А = Е, Или АТ = А–1.

Определение 54. Квадратная матрица А Называется Ортогональной, если

АТ = А–1 (51).

Теорема 48. Линейное преобразование евклидова пространства является ортогональным тогда и только тогда, когда в ортонормированном базисе оно задаётся ортогональной матрицей.

Доказательство Следует из свойства 30 и определения 53.

Теорема 49. Квадратная матрица является ортогональной тогда и только тогда, когда сумма квадратов всех элементов любого столбца (или строки) равна 1, а сумма попарных произведений соответствующих элементов двух различных столбцов (или строк) равна нулю.

Доказательство Следует из формулы 51.

Теорема 50. Линейное преобразование евклидова пространства является ортогональным тогда и только тогда, когда оно ортонормированный базис переводит в ортонормированный базис.

Доказательство. Þ Пусть J : Еn ® Еn ортогональное преобразование и пусть Е = (Е1, Е2, ... , Еn) ортонормированный базис в Еn . Если А – матрица этого преобразования в базисе Е, то А – ортогональная. Но тогда J(Е) = Е×А. Распишем это равенство, если

А = .

Получим J(Ек) = А1кЕ1 + А2кЕ2 + … + АNкЕN . Так как базис Е ортонормированный, то (J(Ек))2 = = (Ек)2 = 1, т. е. все векторы J(Ек) единичной длины. По той же причине (J(Ек), J(Ер)) = А1к×а1р + А2к×а2р + … + АNк×аNр = (Ек , Ер ) = 0,

Если К ¹ р, Т. е. J(Ек) ^ J(Ер). Так как векторы системы J(Е) попарно ортогональны, то они линейно независимы, т. е. J(Е) – базис. Итак, J(Е) – ортонормированный базис.

Ü Пусть Е и J(Е) – ортонормированные базисы. Тогда 1 = (J(Ек))2 = И 0 = (J(Ек), J(Ер)) = А1к×а1р + А2к×а2р + … + Аnк×аnр при К ¹ р. Следовательно, по теореме 49, матрица А – ортогональная.

Теорема 51. Если матрица А Ортогональная, то |А | = ± 1.

Действительно, если матрица А Ортогональная, то АТ× А = Е. Отсюда |АТ×А | = |Е |, |АТ|×| А| = 1, |А|×|А| = 1, |А|2 = 1, |А| = ±1.

Теорема 52. Собственные значения ортогонального преобразования могут быть только 1 или (–1).

Доказательство. Пусть L – собственное значение ортогонального преобразования J.

Тогда существует такой ненулевой вектор (Х1, Х2, … , хN )Т, что А×х = L×х, Где А – матрица преобразования J. Равенство транспонируем и перейдём к сопряжённым числам, получим . Перемножим почленно оба равенства. . Так как А – действительная ортогональная матрица, то . Следовательно, . Отсюда , т. е. |L|2 = 1. Но это и значит, что собственными значениями могут быть только числа 1 и (–1).

Теорема53. Собственные векторы ортогонального преобразования, принадлежащие различным собственным значениям ортогональны.

Доказательство. Для любых А и В из ЕN имеет место (А, В) = (J(А), J(В)) = (L1А, L2В) = = L1L2(А, В). Так как L1 ¹ L2, то, согласно предыдущей теоремы, L1 =1, L2 = –1. Следовательно, (А, В) = – (А, В). Отсюда (А, В) = 0. Так как А и В Не нулевые, то они ортогональные.

< Предыдущая		Следующая >
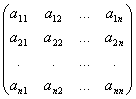