33. Матрица Грама в евклидовом пространстве
Пусть Еn – N-Мерное евклидово пространство и пусть Е = (Е1, Е2, ... , Еn ) – базис в нём. Так как в Еn для любой упорядоченной пары векторов определено их скалярное произведение, то определены скалярные произведения всех пар базисных векторов. Составим из них матрицу
|
Г = |
Матрица Г Называется Матрицей Грама Скалярного произведения для базиса Е. Используя матрицу Грама, можно получить формулу для вычисления скалярного произведения векторов, |
Заданных координатами.
Пусть в базисе Е заданы векторы А = Х1Е1 + Х2Е2 + … + ХnЕn , В = У1Е1+ У2Е2 + … + УnЕn . Тогда (А, в) = (Х1Е1 + Х2Е2 + … + ХnЕn)×( у1Е1+ У2Е2 + … + УnЕn) = ![]() = Х Т×Г×У, где Х Т– строка координат вектора А, У – Столбец координат вектора В . Итак, (А, в) = Х Т×Г×У (42).
= Х Т×Г×У, где Х Т– строка координат вектора А, У – Столбец координат вектора В . Итак, (А, в) = Х Т×Г×У (42).
Свойства матрицы Грама.
10. Матрица Грама симметрична относительно главной диагонали.
Это следует из того, что (Ек, еS ) = (ЕS, ек ).
20. Диагональные элементы матрицы Грама строго положительны.
Это следует из того, что Ек ¹ 0 и, следовательно, (Ек, ек ) > 0.
30. Для матрицы Грама и любого N-Мерного столбца Х Выполняется условие Х Т×Г×Х > 0.
Это следует из 4-ой аксиомы определения скалярного произведения.
Симметрическую матрицу А, Удовлетворяющую условию Х Т×А×Х > 0 для любого
Ненулевого столбца Х, Называют Положительно определённой. Следовательно, матрица
Грама Положительно определённая.
40. Пусть Е = (Е1, Е2, ... , Еn ) и Е1 = (Е11, Е21, ... , Еn1 ) –два базиса в Еn , Г И Г1 – матрицы Грама данного скалярного произведения в базисах Е И Е1 соответственно. Пусть Т – матрица перехода от базиса Е К базису Е1. Тогда (А, в) = Х Т×Г×У, х = Т×х1, у = Т×у1, х Т= (Т×х1)Т= (Х1)Т× ТТ. Следовательно, (А, в) = ((Х1)Т× ТТ)× Г× (Т×у1) = (Х1)Т× (ТТ× Г× Т )× У1. Но (А, в) = (Х1)Т× Г1× у1. Отсюда
Г1 = ТТ× Г× Т (43)
Формула (42) даёт связь матриц Грама в разных базисах.
50. Определители матриц Грама во всех базисах имеют один и тот же знак.
Из формулы (43) следует ú Г1ú =ú ТТú ×úГú ×úТú = úГú ×úТú 2. Так как |Тú 2> 0, то ú Г1ú и ú Гú имеют одинаковые знаки.
60. Все главные миноры матрицы Грама строго положительны.
Примеры.
1. Во множестве М2 Квадратных матриц с действительными элементами скалярное произведение задано формулой 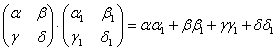 . Найти матрицу Грама этого произведения в базисе Е1 =
. Найти матрицу Грама этого произведения в базисе Е1 = ![]() , Е2 =
, Е2 = ![]() , Е3 =
, Е3 = ![]() , Е4 =
, Е4 = ![]() .
.
Решение. Найдём все попарные произведения базисных элементов: (Е1, е1) = 1, (Е1, е2) = (Е2, е1) = 0, (Е1, е3) = (Е3, е1) = 0, (Е1, е4) = (Е4, е1) = 0, (Е2, е2) = 1, (Е2, е3) = (Е3, е2) = 0, (Е2, е4) = (Е4, е2) = 0, (Е3, е3) = 1, (Е3, е4) = (Е4, е3) = 0, (Е4, е4) = 1. Следовательно,
Г = 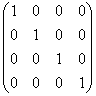 .
.
2. В пространстве R[Х] многочленов степени не выше 3-х скалярное произведение задано формулой ![]() , где A И B – фиксированные действительные числа, A < B. Составить матрицу Грама в базисе (1, Х, х2, х3).
, где A И B – фиксированные действительные числа, A < B. Составить матрицу Грама в базисе (1, Х, х2, х3).
Решение. Найдём все попарные произведения базисных элементов: (1, 1) = ![]() = B – A,
= B – A,
(1, Х) = (Х, 1) = ![]() =
= ![]() ), (1, Х2) = (Х2, 1) =
), (1, Х2) = (Х2, 1) = ![]() =
= ![]() ), (1, Х3) = (Х3, 1) =
), (1, Х3) = (Х3, 1) = ![]() =
= ![]() ), (Х, х) =
), (Х, х) = ![]() =
= ![]() ), (Х, х2) = (Х2, х) =
), (Х, х2) = (Х2, х) = ![]() =
= ![]() ), (Х, х3) = (Х3, х) =
), (Х, х3) = (Х3, х) = ![]() =
= ![]() ), (Х2, х2) =
), (Х2, х2) = ![]() =
= ![]() ), (Х2, х3) = (Х3, х2) =
), (Х2, х3) = (Х3, х2) = ![]() =
= ![]() ), (Х3, х3) =
), (Х3, х3) = ![]() =
= ![]() ). Матрица Грама будет иметь вид:
). Матрица Грама будет иметь вид:
Г = 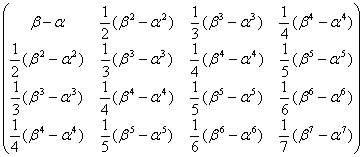 .
.
3. В базисе (Е1, е2, е3) пространства Е3 Скалярное произведение задано матрицей Грама Г =  . Найти скалярное произведение векторов А = (1, –5, 4) и В = (–3, 2, 7).
. Найти скалярное произведение векторов А = (1, –5, 4) и В = (–3, 2, 7).
Решение. Используя формулу (41), получим (А, В) = (1, –5, 4) ×  ×
× ![]() = 7.
= 7.
| < Предыдущая | Следующая > |
|---|
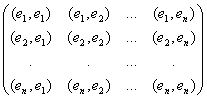 (41)
(41)