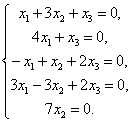25. Область значений и ядро линейного оператора

Пусть J: Ln → Lm линейный оператор.

Определение 33. Областью значений Оператора J Называется множество J (Ln) образов всех элементов из Ln .

Теорема 32. Область значений линейного оператора J: Ln → Lm есть линейное подпространство в Lm

Доказательство. По определению линейного оператора J (Ln) включает Lm. Пусть в и С – любые два вектора из J (Ln). Тогда существуют такие векторы А1 и А2 Из Ln , что J(А1) = В, J (А2) = С. Тогда, по определению 311, J(AА1 + BА2) = AJ(А1) + BJ(А2) = AВ + BС. Так как AА1 + BА2 Î Ln, То J(AА1 + BА2) Î J (Ln), т. е. AВ + BС Î J (Ln). Отсюда следует, что J (Ln) – линейное подпространство в Lm .

Определение 34. Ядром Линейного оператора J: Ln → Lm называется множество всех векторов из Ln , отображающихся в нулевой вектор пространства Lm.

Теорема 33. Ядро линейного оператора J: Ln → Lm является линейным подпространством в пространстве Ln . (Обозначение ядра Ker(J) )

Доказательство. По определению ядра Ker(J) Ì Ln. Если А1 и А2 Î Ker(J), то J (А1) = 0, J (А2) = 0. Но тогда J(AА1 + BА2) = AJ(А1) + BJ(А2) = A×0 + B×0 = 0 Þ AА1 + BА2 Î Ker(J). Итак, Ker(J) – линейное подпространство в пространстве Ln.

Примеры. 1. Даны два линейных пространства L3 И L5 . Пусть Е = (Е1, Е2, е3) и F = (f1, f2, f3 , f4 , f5 ) – базисы в L3 И L5 соответственно. Пусть А1 = (1, 4, –1, 3, 0), А2 = (3, 0, 1, –3, 7), А3 = (1, 1, 2, 2, 0) – три вектора из L5 . Пусть линейный оператор J: L3 ® L5 задан по правилу J(Х1Е1 + Х2Е2 + Х3Е3 ) = Х1А1 + Х2А2 + Х3А3. Найти J(L3) и Ker(J).

Решение. Так как Х1, х2, х3 – любые элементы поля коэффициентов Р, то Х1А1 + Х2А2 + Х3А3 – любой вектор из линейной оболочки < а1, а2, а3 >. Итак, J(L3) = < а1, а2, а3 >.

J(Х1Е1 + Х2Е2 + Х3Е3 ) = 0 Û Х1А1 + Х2А2 + Х3А3 = 0 Û Х1(1, 4, –1, 3, 0) + Х2(3, 0, 1, –3, 7)+ + Х3(1, 1, 2, 2, 0) = (Х1 + 3Х2 + Х3 , 4Х1 + Х3 , –Х1 + Х2 + 2Х3 , 3Х1 –3Х2 + 2Х3 , 7Х2 ) = 0 Û

Для нахождения Х1, х2. х3 получили систему пяти уравнений с тремя неизвестными. Решая её, получим Х1 = х2 = х3 = 0. Следовательно, ядро данного линейного оператора состоит только из нулевого вектора.

2. Даны два линейных пространства L3 И L5 . Пусть Е = (Е1, Е2, е3) и F = (f1, f2, f3 , f4 , f5) – реперы в L3 И L5 соответственно. Пусть линейный оператор J : L5 ® L3 задан правилом J( х1F1 + Х2F2 + Х3 F3 + Х4F4 + Х5F5) = Х1Е1 + Х2Е2 + Х3Е3. Найти J(L5) и Ker(J).

Решение. Очевидно, J(L5) = < е1, Е2, е3 > = L3. Найдём ядро.

J( х1F1 + Х2F2 + Х3 F3 + Х4F4 + Х5F5) = 0 равносильно Х1Е1 + Х2Е2 + Х3Е3 равносильно Х1 = х2 = х3 = 0. Итак, ядро состоит из векторов вида А = (0, 0, 0, Х4, х5 ), где Х4, х5 – любые элементы поля Р.

< Предыдущая		Следующая >