11. Решение матричных уравнений

Рассмотрим простейшие матричные уравнения вида А×Х = В (14) и Х×А = В (15).

Возможны два случая: 1) матрица А Квадратная невырожденная; 2) матрица А - либо вырожденная, либо прямоугольная.

1) Если А – квадратная и |А| ¹ 0, то уравнения (14) и (15) имеют единственное решение каждое: Х = А-1×В и Х = В×А-1 соответственно, если эти произведения определены. И не имеют решения, если они не определены.

2) А – квадратная матрица, но |А| = 0, либо А - прямоугольная матрица. Если матрица А Имеет размерность M´n, а матрица В – Размерность Р´к, то, при M ¹ Р уравнение (14) не имеет решения, а при N ¹ к не имеет решения уравнение (15). Если же M = Р , то в уравнении (14) матрица Х Должна иметь К столбцов, а в уравнении (15) она должна иметь Р Строк. Решение этих матричных уравнений сводится к решению систем линейных уравнений.

Пример 5. Найдите матрицу Х, Если А×Х = В, Где А = , В = .

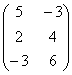Из примера 5 следует, что матрица А Имеет обратную, поэтому Х = А-1×В. Используя найденную в примере 5 матрицу А-1, Получим Х = × = = .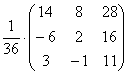

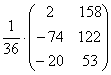Пример 6. Найдите матрицу Х, Если Х×А = В, где А = , В =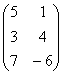. Так как |А| = 0, то для А обратной матрицы нет. По правилам умножения матриц, в матрице В Столько строк, сколько их в матрице Х, И столько столбцов, сколько их в матрице А. Последнее условие выполняется, следовательно, уравнение имеет решение. На матрицу Х накладывается ограничения: в матрице Х Должно быть два столбца и три строки. Чтобы найти элементы такой матрицы, обозначим их и перейдём к системе линейных уравнений. Пусть Х = . Тогда Х×А = . Полученная матрица равна матрице В Тогда и только тогда, когда их соответствующие элементы равны. Получим три системы уравнений. 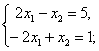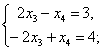Эти системы не имеют решений, следовательно, не имеет решения и данное матричное уравнение.

< Предыдущая		Следующая >