03. Определители. Определители второго и третьего порядков

Одним из источников появления определителей 2-го и 3-го порядков являются системы двух и трёх линейных уравнений с двумя и соответственно тремя переменными.

Пусть дана система (1)

Если обе части первого уравнения умножить на , а второго – на и уравнения почленно вычесть, то получим Аналогично, если первое уравнение умножить на И вычесть из него второе уравнение, умноженное на , то получим Если ¹ 0, то х = у = . Выражения, стоящие в числителях и знаменателях полученных формул, имеют одинаковую структуру. Для их составления используется четыре числа. Если числа, используемые для знаменателя, записать в виде матрицы , то знаменатели получаются по правилу: из произведения элементов одной диагонали таблицы вычитается произведение элементов второй диагонали. Используя отмеченное правило, введём понятие определителя.

Для матрицы диагональ, на которой стоят элементы , называется Главной диагональю, вторая диагональ называется Побочной диагональю.

Определение 2. Определителем 2-го порядка (определителем матрицы ) называется число, равное разности произведения элементов главной диагонали и произведения элементов побочной диагонали.

Определитель матрицы обозначается .

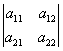Обозначим D = 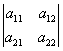, D1 = 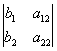, D2 = . Используя определение 2, получим, что система (1) имеет единственное решение тогда и только тогда, когда D ¹ 0. Это решение можно найти по формулам х = , у = (2). Эти формулы называются формулами Крамера.

Пусть дана система трёх уравнений с тремя неизвестными:

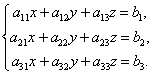(3)

Умножим первое уравнение на , второе уравнение – на 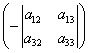, третье уравнение – на и почленно сложим. Получим Х× =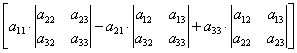

= . Легко заметить, что коэффициент при Х и правая часть составлены из девяти чисел по одному и тому же закону.

Пусть дана матрица А = .

Определение 3. Определителем матрицы А (определителем третьего порядка) называется число, равное D = (4).

Равенство (4) называется разложением определителя по элементам первого столбца. Итак, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка. Если вычислить определители второго порядка, входящие в формулу (4), то получим, что 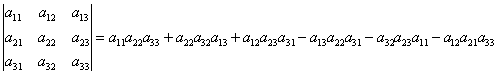(5).

Используя последнюю формулу, непосредственным вычислением можно получить:

1. Определитель не изменится, если в нём строки и столбцы поменять местами (эту операцию называют Транспонированием определителя). Следовательно в определителе строки и столбцы равноправны..

2. D = .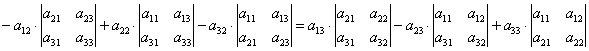

Итак, определитель можно разлагать по любому столбцу. Можно заметить, что знак перед множителем равен . Так как в определителе строки и столбцы равноправны, то аналогичные разложения имеют место и по любой строке определителя (запишите их самостоятельно).

3. Если в определителе одна из строк (или столбцов) целиком состоит из нулей, то определитель равен нулю.

4. Системы (3) имеет единственное решение тогда и только тогда, когда D ¹ 0. Это решение можно найти по формулам: х = , у = , (6),

Где D1, D2, D3 получаются из определителя D заменой первого, второго, третьего столбца соответственно столбцом свободных членов. Формулы (6) тоже называются Формулами Крамера.

< Предыдущая		Следующая >