5.2.3. Гипербола

Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых Фокусами, есть величина постоянная.

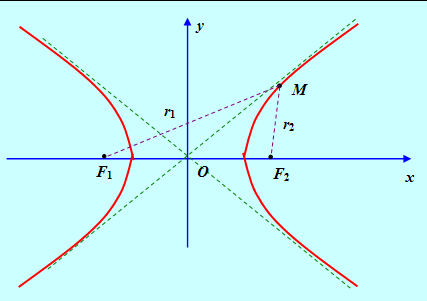
Рис. 2

Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.

|R1 - R2| = 2A, откуда

Если обозначить B² = C² - A², отсюда можно получить

Каноническое уравнение гиперболы.

Эксцентриситетом гиперболы называется величина Е = с / а. Директрисой Di гиперболы, отвечающей фокусу Fi, называется прямая, расположенная в одной полуплоскости с Fi относительно оси Оу Перпендикулярно оси Ох на расстоянии А / е от начала координат.

Свойства гиперболы:

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох Для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями

3) Наряду с гиперболой (2) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением

Для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы E > 1.

5) Отношение расстояния Ri От точки гиперболы до фокуса Fi к расстоянию Di от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Доказательство можно провести так же, как и для эллипса.

< Предыдущая		Следующая >