5.2.4. Парабола

Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F Этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется Фокусом параболы, а прямая – ее Директрисой.

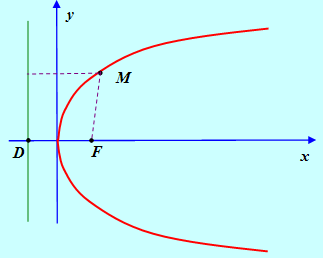
Рис. 3

Для вывода уравнения параболы выберем декартову систему координат так, чтобы ее началом была середина перпендикуляра FD, опущенного из фокуса

На директрису, а координатные оси располагались параллельно и перпендикулярно директрисе. Пусть длина отрезка FD Равна Р. Тогда из равенства R = D следует, что

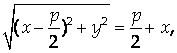
Поскольку

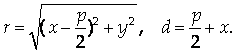
Алгебраическими преобразованиями это уравнение можно привести к виду:

Называемому Каноническим уравнением параболы. Величина Р Называется Параметром Параболы.

Свойства параболы:

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, А вершиной – начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:

Множество точек плоскости, для которых отношение Е Расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при E<1), гиперболу (при E>1) или параболу (при Е=1).

< Предыдущая		Следующая >