5.2.2. Эллипс

Рис. 1

Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых Фокусами, есть величина постоянная.

Замечание. При совпадении точек F1 и F2 эллипс превращается в окружность.

Выведем уравнение эллипса, выбрав декартову систему координат так, чтобы ось Ох Совпала с прямой F1F2, начало координат – с серединой отрезка F1F2. Пусть длина этого отрезка равна 2С, тогда в выбранной системе координат

F1(-C, 0), F2(C, 0). Пусть точка М(х, у) лежит на эллипсе, и сумма расстояний от нее до F1 и F2 равна 2А. Тогда R1 + R2 = 2A, но

Поэтому

Введя обозначение B² = A²-C² и проведя несложные алгебраические преобразования, получим Каноническое уравнение эллипса:

Эксцентриситетом эллипса называется величина Е=с/а. Директрисой Di Эллипса, отвечающей фокусу Fi, называется прямая, расположенная в одной полуплоскости с Fi относительно оси Оу Перпендикулярно оси Ох На расстоянии А/е от начала координат.

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (1), а уравнением второй степени другого вида.

Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2А И 2B (2A>2B), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2) Весь эллипс содержится внутри прямоугольника

3) Эксцентриситет эллипса E < 1. Действительно,

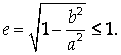
4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно А/е, а Е<1, следовательно, А/е>A, а весь эллипс лежит в прямоугольнике | X |<A, | Y |<B)

5) Отношение расстояния Ri от точки эллипса до фокуса Fi к расстоянию Di от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Доказательство.

Расстояния от точки М(х, у) до фокусов эллипса можно представить так:

Составим уравнения директрис:

Тогда

Отсюда Ri / Di = E, что и требовалось доказать.

< Предыдущая		Следующая >