5.1.5. Приведение квадратичной формы к каноническому виду

Каноническим видом квадратичной формы (8) называется следующий вид:

Покажем, что в базисе из собственных векторов квадратичная форма (8) примет канонический вид. Пусть

Нормированные собственные векторы, соответствующие собственным числам L1,L2,L3 матрицы (10) в ортонормированном базисе . Тогда матрицей перехода от старого базиса к новому будет матрица

В новом базисе матрица А примет диагональный вид (7) (по свойству собственных векторов). Таким образом, преобразовав координаты по формулам:

Получим в новом базисе канонический вид квадратичной формы с коэффициентами, равными собственным числам L1, L2, L3:

Замечание 1. С геометрической точки зрения рассмотренное преобразование координат представляет собой поворот координатной системы, совмещающий старые оси координат с новыми.

Замечание 2. Если какие-либо собственные числа матрицы (10) совпадают, к соответствующим им ортонормированным собственным векторам можно добавить единичный вектор, ортогональный каждому из них, и построить таким образом базис, в котором квадратичная форма примет канонический вид.

Пример 2.

Приведем к каноническому виду квадратичную форму

X² + 5Y² + Z² + 2Xy + 6Xz + 2Yz.

Ее матрица имеет вид

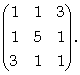
В примере 1 найдены собственные числа и ортонормированные собственные векторы этой матрицы:

Составим матрицу перехода к базису из этих векторов:

(порядок векторов изменен, чтобы они образовали правую тройку). Преобразуем координаты по формулам:

Получим:

Итак, квадратичная форма приведена к каноническому виду с коэффициентами, равными собственным числам матрицы квадратичной формы.

< Предыдущая		Следующая >