5.1.4. Квадратичные формы и их связь с симметрическими матрицами

Квадратичной формой действительных переменных Х1, х2,…,хN называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.

Примеры квадратичных форм:

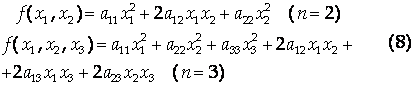
Напомним определение симметрической матрицы:

Квадратная матрица называется Симметрической, если , То есть если равны элементы матрицы, симметричные относительно главной диагонали.

Свойства собственных чисел и собственных векторов симметрической матрицы:

1) Все собственные числа симметрической матрицы действительные.

Доказательство (для N = 2).

Пусть матрица А имеет вид:

Составим характеристическое уравнение:

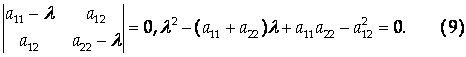
Найдем дискриминант:

Следовательно, уравнение имеет только действительные корни.

2) Собственные векторы симметрической матрицы ортогональны.

Доказательство (для N = 2).

Координаты собственных векторов

Должны удовлетворять уравнениям:

Следовательно, их можно задать так:

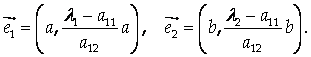
Скалярное произведение этих векторов имеет вид:

По теореме Виета из уравнения (9) получим, что

Подставим эти соотношения в предыдущее равенство:

Значит, .

Замечание. В примере 1 были найдены собственные векторы симметрической матрицы и обращено внимание на то, что они оказались попарно ортогональными.

Матрицей квадратичной формы (8) называется симметрическая матрица

Таким образом, все собственные числа матрицы квадратичной формы действительны, а все собственные векторы ортогональны. Если все собственные числа различны, то из трех нормированных собственных векторов матрицы (10) можно построить базис в трехмерном пространстве. В этом базисе квадратичная форма будет иметь особый вид, не содержащий произведений переменных.

< Предыдущая		Следующая >