5.1.6. Примеры решения задач по теме «Линейные операторы и квадратичные формы»
Задача 1.
Пусть Е1, Е2, Е3, Е4 – базис в векторном пространстве. Разложить вектор
Х = е1 + 2Е2 – Е3 + 3Е4 по новому базису И1, И2, И3, И4, если И1 = Е1,
И2 = Е1 + Е2, И3 = Е1 + Е2 + Е3, И4 = Е1 + Е2 + Е3 + Е4.
Указание
Выпишите матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе. Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.
Выпишем матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе:
 .
.
Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.
Координаты вектора Х в старом базисе: Х = (1; 2; -1; 3). Пусть в новом базисе он имеет координаты: X = (X, Y, Z, T). Тогда, используя матрицу Т, найдем связь между старыми и новыми координатами:
 .
.
Следовательно, в новом базисе Х = (-1; 3; -4; 3).
Ответ: Х = (-1; 3; -4; 3).
Задача 2.
Найти матрицу А’ оператора А:

В базисе И1 = Е1 + Е3, И2 = 2Е1 + Е2, И3 = Е1 + Е2 + Е3.
Указание
Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому.
Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому. Составим матрицу Т :
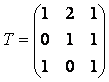 .
.
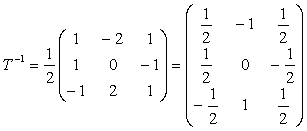 .
.
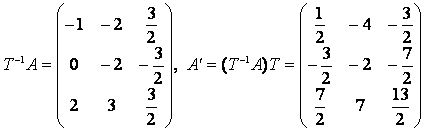 .
.
Ответ:  .
.
Задача 3.
Найти собственные числа и собственные векторы линейного оператора, заданного матрицей
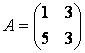 .
.
Указание
Для определения собственных чисел составьте характеристическое уравнение:
![]()
Координаты собственных векторов RI = (Xi, Yi) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке LI.
Решение
Составим характеристическое уравнение:

Найдем собственные векторы:
1) для L = -2 координаты собственного вектора R1 = (X1, Y1) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке L = -2:
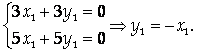
Если Х1 = 1, то У1 = -1, и R1= (1; -1). Остальные собственные векторы коллинеарны вектору (1; -1), и общий вид собственного вектора, соответствующего L = -2: R1 = С1(1; -1), где С1 – произвольная постоянная.
2) для L = 6 координаты собственного вектора R2 (X2; Y2) удовлетворяют системе:
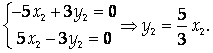
Пусть Х2 = 3, тогда У2 = 5, и R2 = (3; 5). Соответственно общий вид второго собственного вектора: R2 = С2(3; 5).
Ответ: собственные числа L1 = -2, L2 = 6; собственные векторы R1 = С1(1; -1),
R2 = С2(3; 5).
Задача 4.
В пространстве 3-мерных векторов задан оператор
AX = (Xi)I,
Где I – базисный вектор декартовой системы координат.
Выяснить геометрический смысл этого оператора.
Указание
Множитель Xi – скалярное произведение, то есть число, поэтому вектор (Xi)I коллинеарен оси Ох.
Решение
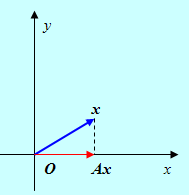
Рис. 1
Оператор А переводит произвольно направленный вектор Х в вектор
KI, коллинеарный оси Ох, поскольку первый множитель – скалярное произведение, то есть число. Из определения скалярного произведения следует, что
AX = (Xi)I = (|X|·|I|·cosφ) I = (|X|cosφ)I.
Следовательно, А – оператор проектирования на ось Ох.
Ответ:
Оператор осуществляет проектирование вектора Х на ось Ох;
Задача 5.
Привести матрицу А линейного оператора к диагональному виду и найти соответствующий базис, если
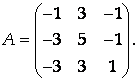
Указание
Найдите собственные числа и собственные векторы матрицы линейного оператора, задайте базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид, и составьте матрицу перехода к новому базису.
Решение
Характеристическое уравнение:
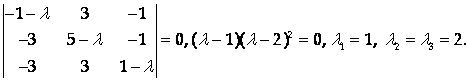
Найдем собственные векторы, соответствующие полученным собственным числам.
При L = 1 для вектора R1 = (X1, Y1, Z1) получаем:

Подставим в строки определителя L = 2 и найдем связь между координатами собственного вектора R2 = (X2, Y2, Z2):

Та же зависимость получается для координат третьего собственного вектора R3 = (X3, Y3, Z3). Выберем значения двух координат каждого из этих векторов так, чтобы R2 и R3 были линейно независимы.
Пусть Х2 = 1, У2 = 0, тогда Z2 = -3, и R2 = (1; 0; -3).
Для R3 выберем Х3 = 0, У3 = 1, тогда Z3 = 3, R3 = (0; 1; 3).
Получен базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид.
Составим матрицу перехода к новому базису:
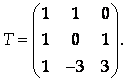
Найдем матрицу, обратную к Т:
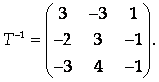 .
.
Тогда в базисе из собственных векторов матрица оператора
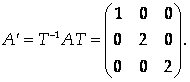
Ответ: в базисе (1; 1; 1), (1; 0; -3), (0; 1; 3) матрица оператора
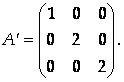
Задача 6.
Линейный оператор А задан в некотором базисе матрицей
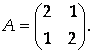
Найти собственные числа и собственные векторы оператора А-1 – оператора, обратного к А.
Указание
Собственные числа обратного оператора являются обратными к собственным числам данного оператора, а их собственные векторы одинаковы.
Решение
Характеристическое уравнение для А:

Собственные векторы: для L = 3 R1 = C(1; 1), для L = 1 R2 = C(1; -1).
Найдем матрицу обратного оператора:
 .
.
Соответствующее характеристическое уравнение:
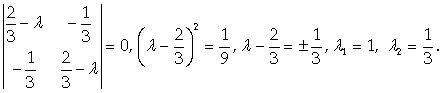
Собственные векторы: для L = 1 R1 = C(1; -1), для L = 1/3 R1 = C(1; 1).
Ответ: L1 = 1, L2 = 1/3, R1 = C(1; -1), R2 = C(1; 1).
Задача 7.
Составить матрицу квадратичной формы 3Х2 – 10Ху + 8У2 и найти ее собственные числа.
Указание
Матрица квадратичной формы А11Х2 + 2А12Ху + А22У2 является
Симметрической (Aij = Aji) и имеет вид:

Решение
В нашей задаче А11 = 3, А12 = -5, А22 = 8. Следовательно,
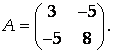
Составим характеристическое уравнение, корнями которого являются собственные числа:

Ответ: матрица квадратичной формы  ,
,
Собственные числа ![]()
Задача 8.
Найти базис, в котором квадратичная форма 2Х2 + 4Ху + 5У2 будет иметь канонический вид, и указать этот вид.
Указание
Канонический вид квадратичной формы:
1) во-первых, не содержит произведения Ху;
2) во-вторых, коэффициенты при Х2 и У2 равны собственным числам матрицы квадратичной формы.
Базис, в котором квадратичная форма имеет канонический вид, состоит из нормированных собственных векторов матрицы квадратичной формы.
Решение
Матрица квадратичной формы
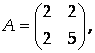
Характеристическое уравнение
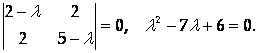
Собственные числа: L1 = 1, L2 = 6.
Собственные векторы:
Для L1 = 1 координаты вектора R1 = {X1, Y1} определяются уравнением
Х1 + 2У1 = 0, Х1 = -2У1. Если У1 = 1, то Х1 = -2, и R1 = C{-2; 1}. Найдем значение С из условия, что вектор R1 нормирован, то есть его длина равна 1:

Аналогично для L2 = 6: R2 = {X2, Y2}, -4Х2 + 2У2 = 0, R2 = C{1; 2}.

Итак, базис имеет вид:
![]()
И в этом базисе квадратичная форма примет вид: L1Х2 + L2У2, то есть Х2 + 6У2.
Ответ: в базисе ![]() квадратичная форма имеет канонический вид: Х2 + 6У2.
квадратичная форма имеет канонический вид: Х2 + 6У2.
Задача 9.
Указать преобразование координат, приводящее квадратичную форму
8Х2 – 12Ху + 17У2 к каноническому виду.
Указание
Матрица преобразования координат имеет вид:
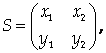
Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы.
Решение
Найдем базис из нормированных собственных векторов.

Составим матрицу перехода к новому базису, столбцами которой будут координаты новых базисных векторов R1, R2 в старом базисе:
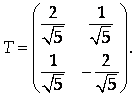
Строки этой матрицы определяют коэффициенты уравнений, выражающих старые координаты через новые:

Где Х, У – координаты в старом базисе, а Х’, Y’ – в новом.
Таким образом, найдено искомое преобразование.
Ответ: 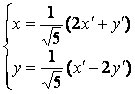 .
.
Задача 10.
Привести к каноническому виду квадратичную форму 5Х2 – 12Ху.
Указание
Матрица преобразования координат имеет вид:
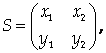
Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы. В новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.
Решение

Матрица перехода к базису из собственных векторов:
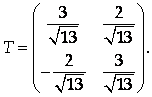
Преобразование координат:
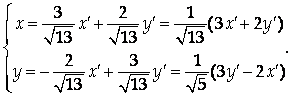
Подставим найденные выражения в квадратичную форму:
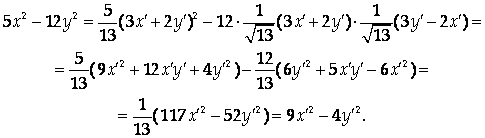
Как и следовало ожидать, в новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.
Ответ: 9Х2 – 4У2.
Задача 11.
Найти преобразование координат, приводящее квадратичную форму
X2 + Y2 + 5Z2 – 6Xy + 2Xz – 2Yz к каноническому виду.
Указание
Матрица квадратичной формы A11X2 + A22Y2 + A33Z2 + 2A12Xy + 2A13Xz + 2A23Yz имеет вид:

Матрица преобразования координат:

Где R1 = (X1, Y1, Z1), R2 = (X2, Y2, Z2) и R3 = (X3, Y3, Z3) – нормированные собственные векторы.
Решение.
Матрица квадратичной формы A11X2 + A22Y2 + A33Z2 + 2A12Xy + 2A13Xz + 2A23Yz имеет вид:

Для заданной квадратичной формы

Составим и решим характеристическое уравнение:
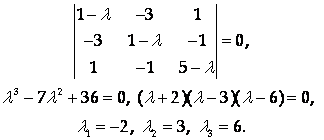
(Мы не останавливаемся подробно на способах решения уравнений высших порядков. В данном случае, например, один из корней был найден перебором делителей свободного члена, а затем левая часть разложена на множители.)
Найдем нормированные собственные векторы:



Матрица перехода к новому базису:

Задает преобразование координат:

Заметим, что в новых координатах квадратичная форма примет вид:
![]()
Где коэффициенты являются собственными числами, стоящими в той же последовательности, что и соответствующие собственные векторы в матрице Т.
Ответ: 
| < Предыдущая | Следующая > |
|---|