4.1.1. Прямые и плоскости. Уравнение прямой на плоскости. Общее уравнение прямой на плоскости

Пусть на плоскости задана декартова прямоугольная система координат. Говорят, что соотношение (или уравнение)

Задает множество точек L на плоскости, если для любой точки М L ее координаты удовлетворяют равенству (1), и наоборот, если для всех пар (Х,У), удовлетворяющих (1), точка М = {X, Y} принадлежит множеству L. При этом говорят, что уравнение (1) является уравнением множества L.

Пусть на плоскости дана точка М0 = {X0, Y0}. Найдем уравнение прямой L, проходящей через эту точку перпендикулярно вектору П = (А, В). Пусть М = {X, Y} – произвольная точка на прямой L. Тогда

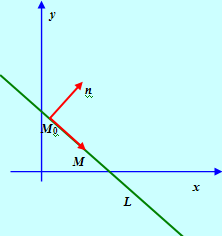
Рис. 1

Тем самым уравнение прямой L задается в виде

Где С = -Ах0 – Ву0.

Нормальным вектором Прямой называется любой ненулевой вектор, перпендикулярный этой прямой.

Пример 1. Найдем уравнение прямой с нормальным вектором П = (-3, 2), проходящей через точку M0 = {2, 1}. Имеем

-3(Х – 2) + 2(У – 1) = 0

Или

-3Х + 2У + 4 = 0.

Теорема 9.1. Всякая прямая на плоскости может быть задана уравнением

И любое уравнение (3) задает на плоскости некоторую прямую. При этом вектор П = (А, В) является нормальным вектором этой прямой.

Доказательство.

Пусть дана произвольная прямая. Выберем на ней точку М0 = {X0, Y0}. Пусть П = (А, В) – некоторый нормальный вектор этой прямой. Тогда, как было показано выше, уравнение этой прямой запишется в виде (3).

Покажем, что всякое уравнение (3) определяет некоторую прямую на плоскости. Найдем точку М0 = {X0, Y0}, координаты которой удовлетворяют уравнению

Если А 0, то, например, можно положить

А если В 0, то

Теперь построим прямую с нормальным вектором П = (А, В), проходящую через точку М0. Ее уравнение будет иметь вид

Раскрывая скобки, приходим к уравнению (3).

Уравнение (3) называется Общим уравнением прямой На плоскости.

< Предыдущая		Следующая >