4.1.2. Неполные уравнения прямой
Если хотя бы один из коэффициентов уравнения (3) равен нулю, то такое уравнение называется Неполным.
1. Предположим, что С = 0, т. е. уравнение прямой задается в виде
![]()
Такая прямая (см. рис. 2) проходит через начало координат, так как координаты точки О = {0,0} удовлетворяют уравнению этой прямой.
2. Пусть А = 0 (при этом В![]() 0). Тогда прямая (см. рис. 3) параллельна оси Ох, так как ее нормальный вектор П = (0, В) коллинеарен вектору I. Ее уравнение может быть записано в виде
0). Тогда прямая (см. рис. 3) параллельна оси Ох, так как ее нормальный вектор П = (0, В) коллинеарен вектору I. Ее уравнение может быть записано в виде
![]()
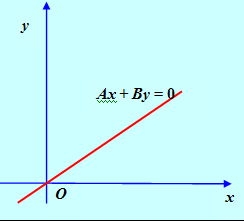
Рис. 2
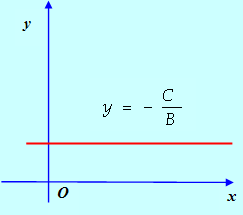
Рис. 3
3. Пусть В = 0 (при этом А![]() 0). Тогда прямая (см. рис. 4) параллельна оси Оу, так как ее нормальный вектор П = (А,0) коллинеарен вектору J. Ее уравнение может быть записано в виде
0). Тогда прямая (см. рис. 4) параллельна оси Оу, так как ее нормальный вектор П = (А,0) коллинеарен вектору J. Ее уравнение может быть записано в виде
![]()
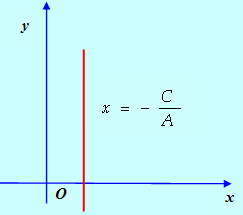
Рис. 4
| < Предыдущая | Следующая > |
|---|