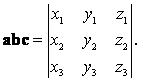3.2.3. Векторное и смешанное произведения векторов, заданных координатами
Пусть A = x1I + y1J + z1K, a B = X2I + y2J + z2K. Тогда

Будем считать, что система координат правая. Тогда
[I,J] = K, [J,K] = I, [K,I] = J.
Учитывая, что при перемене множителей векторное произведение меняет знак, получаем
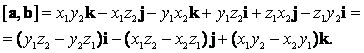 (1)
(1)
Формулу (1) удобно записать в виде символического определителя

(для получения формулы надо раскрыть определитель по первой строке).
Пример 2.
Найдем площадь треугольника с вершинами в точках A = {2, 2, -3},
B = {1, 3, -3} и C = {1, 2, -1}. Площадь этого треугольника S равна половине площади параллелограмма, построенного на векторах АВ и АС. Следовательно,
![]()
Имеем
![]()
Поэтому
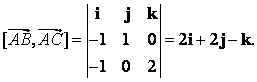
Отсюда
![]()
Упражнение 1.
При каких значениях A и B вектор A I + B J + K будет коллинеарен вектору
[A, B], если А = (2, -1, 1), а B = (1, 2, -2)?
Найдем координаты вектора [A, B]:

Поскольку координаты коллинеарных векторов пропорциональны, числа A и B должны удовлетворять равенствам
![]()
Откуда A = 0, B = 1.
Пусть теперь A = (X1, Y1, Z1), B = (X2, Y2, Z2), а С = A = (X3, Y3, Z3). Тогда
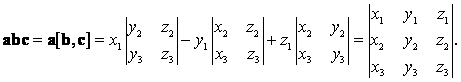
Тем самым смешанное произведение векторов вычисляется по формуле
|
|
Пример 3. Выясним, какую тройку: правую или левую – образуют векторы А = (1, 1, 0), B = (-1, 2, 1) и С = (-3, -2, 0). Для этого найдем смешанное произведение

Из того, что Abc < 0, вытекает, что тройка A, B, C – левая.
Упражнение 2.
При каком A векторы А = (-1, 1, A), B = (2, 1, 0) и С = (3, 1, 1) являются компланарными?
Смешанное произведение компланарных векторов равно нулю, поэтому
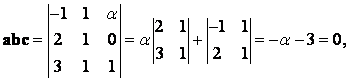
Откуда A = -3.
| < Предыдущая | Следующая > |
|---|