3.2.2. Смешанное произведение
Смешанным произведением трех векторов A, B и С называется величина
|
Abc = a [B,C] |
(скалярное произведение векторов А и [B,C]).
Векторы называются Компланарными, если существует плоскость, параллельная им.
Из определения векторного произведения вытекает, что векторы A, B и С компланарны в том и только в том случае, если А ^ [B,C]. Тем самым
|
Abc = 0 |
Тройка некомпланарных векторов A, B и С называется Правой, если угол меду векторами А и [B,C] – острый. В противном случае тройка называется Левой. Множество всех систем декартовых прямоугольных координат распадается на два класса. Один класс – правые системы координат, в которых тройка базисных векторов I, J, K – правая, другой класс – левые системы координат, в которых тройка базисных векторов I, J, K – левая.

Рис. 4
На рис. 4 А) – правая система координат, а B) – левая система координат.
Смешанное произведение обладает следующими свойствами:
1. Для некомпланарных векторов
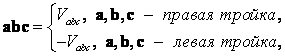
Где VAbc – объем параллелепипеда, построенного на векторах A, B и С.

Рис. 5
Доказательство.
Объем параллелепипеда, построенного на векторах A, B и С, равен произведению площади основания |[B,C]| на высоту H = |A||cos Q|, где Q - угол между векторами А и [B,C] (см. рис. 8.5). Поэтому
![]()
Знак смешанного произведения совпадает со знаком cos Q, который положителен, если тройка правая, и отрицателен в противном случае.
2. Для любых векторов A, B и С
Abc = bca = cab = – acb = – cba = – bac.
Доказательство.
Из предыдущего свойства вытекает, что при перестановке сомножителей в смешанном произведении может измениться лишь знак произведения. Остается заметить, что тройки, получаемые по схеме из рис. 8.6 (начиная с любого вектора), имеют одинаковую ориентацию. При движении по этой схеме в противоположном направлении ориентация меняется.
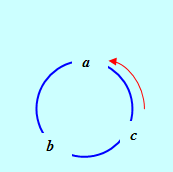
Рис. 6
3. (L1A1 + L2 A2)Bc = L1A1Bc + L2 A2Bc.
Доказательство.
Пользуясь свойствами скалярного произведения, получаем:

Аналогичное свойство имеет место для остальных множителей:
А(L1B1 + L2 B2)C = L1Ab1C + L2 Ab2C,
Ab(L1C1 + L2 C2) = L1Abc1 + L2 Abc2.
Доказательство.
Имеем
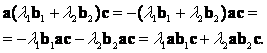
Аналогично доказывается второе равенство.
Докажем теперь свойство 4 векторного произведения, т. е. равенство
[A + B, с] = [А, с] + [B,с].
Доказательство.
Из свойства 3 смешанного произведения вытекает, что для любого вектора Е
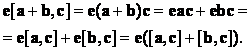
Выбирая в качестве Е векторы I, J и K, получаем, что координаты векторов
[A + B, C] и [A, C] + [B, C] совпадают. Из этого следует, что эти векторы равны.
| < Предыдущая | Следующая > |
|---|