3.2.1. Векторное и смешанное произведения. Векторное произведение

Векторным произведением векторов А и B называется вектор [A,B] такой, что:

1. |[A,B]| = |A||B| sin J, где J – угол между векторами А и B.

2. [A,B] ^ A, [A,B] ^ B.

3. Вектор [A,B] направлен так, что из конца этого вектора кратчайший поворот от вектора А к вектору B происходит против часовой стрелки.

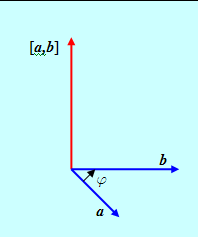
Рис. 1

Из п.1 определения векторного произведения вытекает, что

[A,B] = 0 A || B.

Векторное произведение обладает следующими свойствами:

1. |[ A,B]| = SAb , где SAb – площадь параллелограмма, построенного на векторах А и B.

Доказательство.

Если J - угол между векторами А и B, то (см. рис. 2)

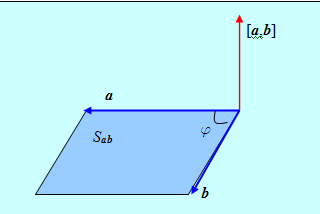
Рис.2

2. |[ A,B]| = – |[ B,а]|.

3. |[ LA,B]| = L|[ A,B]|.

Числовой множитель можно выносить и из второго множителя. Действительно,

|[ A,LB]| = – |[ LB,а]| = – L|[ B,а]| = L|[ A,B]|.

4. [A + B, с] = [А, с] + [B,с].

Доказательство этого свойства будет дано в следующем пункте.

Пример 1. Вычислим произведение [A + B, A – B]. Пользуясь тем, что [A, A] = [B,B] = 0 (как произведение коллинеарных векторов), будем иметь:

[A + b, a – b] = [B,А] - [A, b] = 2[B, a].

Отсюда

SAb = ½ |[A + b, a – b]| = ½ |A + b||A – b| SinA,

Где A – угол между векторами A + B и A – B.

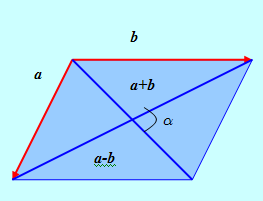
Рис. 3

Тем самым доказано, что площадь параллелограмма равна половине произведения длин диагоналей на синус угла между ними.

< Предыдущая		Следующая >