3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»

Задача 1.

Даны векторы А = (-2; 3; 5) и B = (4; -1; 7). Найти координаты вектора

3А – 2B.

Указание

При умножении вектора на число все его координаты

Умножаются на это число, при сложении векторов складываются их соответствующие координаты.

Решение

3А = (-6; 9; 15), -2B = (-8; 2; -14).

3А – 2B = 3А + (-2B) = (-6 - 8; 9 + 2; 15 – 14) = (-14; 11; 1).

Ответ: 3А – 2B = (-14; 11; 1).

Задача 2.

При каких A И B векторы А = (A; 3; -5) и B = (1; -2; B) коллинеарны?

Указание

Координаты коллинеарных векторов пропорциональны.

Решение

Если A || B, то . Отсюда:

Ответ: .

Задача 3.

Найти направляющие косинусы вектора А = {-2; -1; 2}.

Указание

Направляющие косинусы являются координатами орта (единичного вектора) данного направления.

Решение

Найдем модуль вектора А:

Разделив все координаты вектора А на его модуль, получим координаты орта:

Следовательно,

Ответ:

Задача 4.

Разложить вектор D = { -6; 0; 13} по базису из векторов A = {2; -1; 3},

B = {1; 1; -1}, C = {-3; 1; 2}.

Указание

Требуется найти такие числа A, B, G, что D =AA + BB + GC. Задайте координаты вектора AA + BB + GC и приравняйте их соответствующим координатам вектора D.

Решение

Требуется найти такие числа A, B, G, что D =AA + BB + GC. Зададим координаты векторов AA, BB, GC: αA = {2A; -A; 3A},

BB = {B; B; -B}, GC = {-3G; G; 2G}.

Тогда AA + BB + GC = {2A + B- 3G; -A + B+ G; 3A - B+ 2G}, причем координаты этого вектора должны равняться соответствующим координатам вектора D. Приравнивая эти координаты, получаем систему уравнений для определения A, B, G:

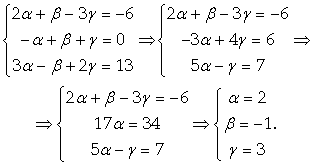
Следовательно, D = 2A – B + 3C.

Ответ: D = 2A – B + 3C.

Задача 5.

Для векторов A = {1; -2; 3}, B = {-1; 1; -2}, C = {3; 2; 1}, D = { 15; 7; 4} найти такие числа A, B, G, чтобы векторы AA, BB, GC и D образовали замкнутую ломаную линию, если начало каждого последующего вектора совместить с концом предыдущего.

Указание

Для выполнения условия задачи сумма векторов AA + BB + GC + D должна равняться нулю.

Найдите координаты вектора AA + BB + GC + D и приравняйте нулю каждую из них.

Решение

Для выполнения условия задачи сумма векторов AA + BB + GC + D должна равняться нулю.

Найдем координаты вектора AA + BB + GC + D:

AA + BB + GC + D = {A – B + 3G + 15; 2A + B + 2G + 7; 3A - 2B + G +4}. Следовательно, A, B и G,должны быть решением системы уравнений

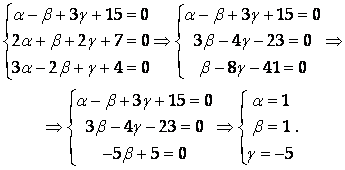
Ответ: A = B = 1, G = -5.

Задача 6.

Выяснить, является ли система векторов A = {2; -3; 1}, B = {3; -1; 5},

C = {1; -4; 3} линейно зависимой или линейно независимой.

Указание

Система векторов называется линейно независимой, если равенство

AA + BB + GC = 0

Верно только при A = B = G = 0.

Решение

Координаты вектора AA + BB + GC имеют вид:

AA + BB + GC = {2A +3B + G; -3A - B - 4G; A + 5B + 3G}.

Вычислим главный определитель Δ системы уравнений

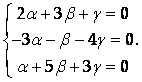
По правилу Крамера система имеет единственное решение, но для однородной системы всегда существует нулевое решение (A = B = G = 0).

Поскольку других решений нет, данная система векторов линейно независима.

Ответ: Система векторов линейно независима.

Задача 7.

Найти координаты какого-либо вектора, направленного по биссектрисе угла между векторами А = (-4; 3; 0) и B = (12; -15; 16).

Указание

Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.

Решение

Вектор A + B направлен по диагонали параллелограмма, построенного на векторах А и B как на смежных сторонах и выходящей из общего начала векторов А и B.

Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.

Следовательно, |5A| = |B|. Значит, параллелограмм со сторонами, совпадающими с векторами 5A и B, является ромбом, поэтому вектор 5A + B будет иметь заданное направление.

5A + B = (-20 + 12; 15 – 15; 0 + 16) = (-8; 0; 16).

Ответ: (-8; 0; 16).

Задача 8.

При каких значениях X, Y, Z точки А(Х; -1; 3), В(5; -4; Z), C(-2; Y; 9), D(-5; 1; 7) являются вершинами параллелограмма?

Указание

Для выполнения условия задачи требуется коллинеарность векторов и и и .

Решение

Для выполнения условия задачи требуется коллинеарность векторов и и и .

Найдем координаты этих векторов:

Из последней пропорции получаем, что Z = 1 – 2Y. Тогда

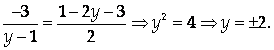
Но при этих значениях неизвестных

Условие задачи выполнено.

Ответ: Х = 2, У = -2, Z = 5.

Задача 9.

Найти скалярное произведение (A – B)(2A + B), если |A| = 2, |B| = 3, а угол между А и B равен 120о.

Указание

Используйте определение скалярного произведения:

Ab = |A|·|B|·cosφ.

Решение

Используем свойства скалярного произведения:

(A – B)(2A + B) = 2Аа – 2Ba + Ab – Bb = 2|A|2 – Ab - |B|2.

По определению скалярного произведения

Ab = |A|·|B|·cosφ = 2·3·(-½) = -3.

Тогда (A – B)(2A + B) = 2·4 – (-3) – 9 = 8.

Ответ: (A – B)(2A + B) = 8.

Задача 10.

Известно, что |A| = 3, |B| = |C| = 1 и A + B + C = 0. Найти Ab + Bc + Ca.

Указание

Вектор A + B + C – нулевой, поэтому его скалярное произведение с любым вектором равно нулю. Умножьте скалярно вектор A + B + C сначала на A, затем на B И на C.

Решение

Вектор A + B + C – нулевой, поэтому его скалярное произведение с любым вектором равно нулю. Умножим скалярно вектор A + B + C сначала на A, затем на B И на C. Получим:

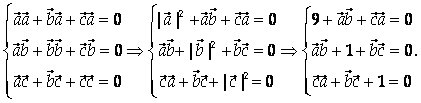
Сложим левые и правые части полученных равенств:

11 + 2Ab + 2Bc + 2Ca = 0, откуда Ab + Bc + Ca = -5,5.

Ответ: Ab + Bc + Ca = -5,5.

Задача 11.

Даны векторы А = {2; -3; 1} и B = {-1; 2; 1}. Найти скалярное произведение

(3А – B)(A + 2B).

Указание

Найдите координаты векторов 3А – B и A + 2B или используйте свойства скалярного произведения.

Решение

1-й способ.

Найдем координаты векторов 3А – B и A + 2B:

3А – B = {3·2 + 1; 3·(-3) - 2; 3·1 - 1} = {7; -11; 2};

A + 2B = {2 + 2·(-1); -3 + 2·2; 1 + 2·1} = {0; 1; 3}.

Тогда (3А – B)(A + 2B) = 7·0 - 11·1 + 2·3 = -5.

2-й способ.

Используем свойства скалярного произведения:

(3А – B)(A + 2B) = 3Aa – Ba +6Ab – 2Bb = 3|A|2 + 5Ab -2|B|2.

|A|2 = 22 + (-3)2 + 12 = 14;

|B|2 = (-1)2 + 22 + 12 = 6;

Ab = 2·(-1) - 3·2 + 1·1 = -7;

(3А – B)(A + 2B) = 3·14 + 5·(-7) - 2·6 = -5.

Ответ: (3А – B)(A + 2B) = -5.

Задача 12.

Найти косинус угла между векторами А = {2; -2; -1} и B = {-6; 3; 2}.

Указание

Используйте формулу, выражающую косинус угла между векторами через их скалярное произведение.

Решение

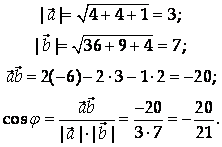
Ответ: .

Задача 13.

Найти вектор B, если А = {2; -2; 3}, B || A И Ab = -51.

Указание

Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = {2K; -2K; 3K}.

Решение

Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = {2K; -2K; 3K}.

Тогда Ab = 2·2K – 2(-2K) + 3·3K = 17K = -51, откуда K = -3, B = {-6; 6; -9}.

Ответ: B = {-6; 6; -9}.

Задача 14.

Известно, что |A| = 2, |B| = 7. Найти значения K, при которых векторы

A + KB и A - KB перпендикулярны.

Указание

Если векторы перпендикулярны, то их скалярное произведение равно нулю.

Решение

Если векторы перпендикулярны, то их скалярное произведение равно нулю.

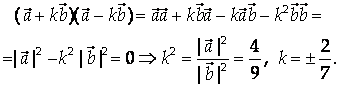
Ответ: K = .

Задача 15.

Найти проекцию вектора А = {7; 0; -5} на ось, образующую с координатными осями Ох и Оу углы 60о и 45о, а с осью Oz – тупой угол γ.

Указание

Используйте свойство направляющих косинусов:

Cos2α + cos2β + cos2γ = 1

Решение

Найдем cosγ: cos260o + cos245o + cos2γ = 1,

Тогда проекция А на заданную ось равна:

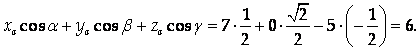
Ответ: 6.

< Предыдущая		Следующая >