3.1.3. Координаты вектора и точки

Зафиксируем в пространстве некоторую точку О и три взаимно перпендикулярных вектора единичной длины I, J И K.

Рис. 7

Совокупность точки О и векторов I, J, K называется Декартовой прямоугольной системой координат. Прямые, проходящие через точку О параллельно векторам I, J И K, называются Координатными осями и носят названия осей Абсцисс (Ох), Ординат (Оу) и Аппликат (Oz) соответственно.

Пусть задан вектор А. Совместим его начальную точку с началом координат О, а через его конечную точку А проведем плоскости, перпендикулярные координатным осям. Пусть эти плоскости пересекают оси Ox, Oy, Oz в точках L, M, N соответственно.

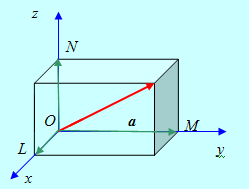
Рис. 8

Нетрудно убедиться, что

Поскольку вектора коллинеарны векторам I, J, K соответственно, то найдутся числа X1, Y1, Z1 такие, что

Следовательно, любой вектор А может быть представлен в виде

A = X1I + Y1J + Z1K. (1)

Представление (1) единственно. Действительно, если предположить, что наряду с (1) существует другое представление

A = X′1I + Y′1J + Z′1K,

То, вычитая это равенство из (7.1), получим

0 = (X1 – X′1)I + (Y1 – Y′1)J + (Z1 – Z′1)K.

Если Х1 ≠ Х′1, то

Что невозможно, т. к. вектор в правой части лежит в плоскости, параллельной осям Оу и Oz, а вектор I перпендикулярен этой плоскости. Следовательно,

Х1 = Х′1. Аналогично доказывается, что Y1 = Y′1 и Z1 = Z′1.

Числа X1, Y1, Z1 в представлении (1) называются Координатами вектора А. Вместе с равенством (1) будет использоваться также запись вида

A = (X1, Y1, Z1).

Радиусом-вектором точки А называется вектор, начало которого совпадает с началом координат О, а конец – с точкой А. Координатами точки А называются координаты радиус-вектора точки А. При этом, если

= (X1, Y1, Z1), будем писать

А = { x1, Y1, Z1}.

< Предыдущая		Следующая >