3.1.2. Линейные операции над векторами
1. Сложение векторов. Пусть даны векторы А и B. Совместим начальную точку вектора B с конечной точкой вектора А. Тогда вектор, начальная точка которого совпадает с начальной точкой вектора А, а конечная – с конечной точкой B, называется Суммой векторов А + B.
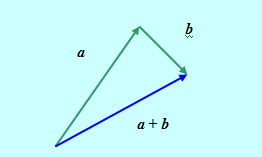
Рис. 3
Совместим начальные точки векторов А и B и обозначим эту точку через О. Построим параллелограмм ОАСВ на сторонах этих векторов. Тогда вектор ![]() A + B. Тем самым получено эквивалентное определение суммы векторов, называемое Правилом параллелограмма.
A + B. Тем самым получено эквивалентное определение суммы векторов, называемое Правилом параллелограмма.
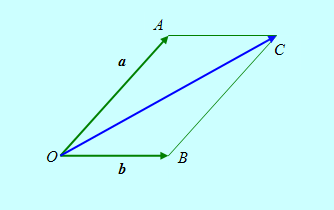
Рис. 4
Из рис. 4 видно, что
![]()

Рис. 5
Таким образом, операция сложения векторов коммутативна:
A + B = B + A.
Имеет место также свойство ассоциативности:
(А + B) + C = A + (B + C).
2. Умножение вектора на число. Произведением вектора А на число L Называется вектор LА такой, что:
1. |LA| = |L||A|.
2. LA || A, и оба вектора одинаково направлены, если L > 0, и имеют противоположные направления, если L < 0.

Рис. 6
Таким образом, если А не равен нулю и A || B, то найдется число L такое, что B =LA. Достаточно взять
![]()
Где E = 1, если А и B одинаково направлены, и E = -1, если А и B имеют противоположные направления.
Отметим основные свойства операции умножения вектора на число, которые непосредственно вытекают из определения этой операции:
1. (L + M)А = LА + MА.
2. L(MА) = (LM)А.
3. L(A + b) = LA + LB.
3. Вычитание векторов. Разностью Двух векторов А и B называется вектор
A – B = A + (-1)·B.
| < Предыдущая | Следующая > |
|---|