3.1.1. Аналитическая геометрия. Векторная алгебра
Пусть даны две точки А и В. Отрезок, соединяющий эти точки, будем называть Направленным, если указаны начальная и конечная точка отрезка, т. е. на отрезке указано направление.
Вектором называется направленный отрезок. Векторы будем обозначать буквами А, B, C,… или, указывая начальные и конечные точки,
![]() .
.
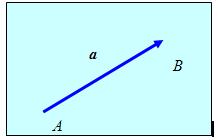
Рис.1
Вектор называется Нулевым, если начальная и конечная точки совпадают. В этом случае будем писать А = 0. Длиной Вектора называется длина соответствующего ему направленного отрезка. Длина обозначается через | A | или ![]() .
.
Векторы А и B называются Коллинеарными (при этом пишут A || B), если существует прямая, которой они параллельны. Нулевой вектор считается коллинеарным любому вектору.
Два вектора называются Равными, если они коллинеарны, одинаково направлены и имеют равные длины. Иными словами, мы рассматриваем Свободные Векторы, начальные точки которых могут выбираться произвольным образом.

Рис. 2
| < Предыдущая | Следующая > |
|---|