2.3.6. Примеры решения задач по теме «Системы уравнений общего вида. Метод Гаусса»
Задача 1.
Указать базисный минор матрицы
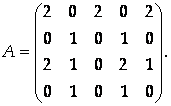
Указание
Определите вначале ранг матрицы А, а затем найдите ненулевой минор, порядок которого равен R(A).
Определим R(A). Вторая и четвертая строки А равны, поэтому после вычитания из 4-й строки 2-й получаем:

Вычислим минор полученной матрицы, составленный из первых трех столбцов:

Таким образом, найден минор максимально возможного (3-го) порядка, не равный нулю. Следовательно, ранг матрицы А равен рангу преобразованной матрицы, то есть равен 3, а рассмотренный минор является базисным.
Ответ: 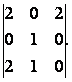
Задача 2.
Определить количество решений системы линейных уравнений
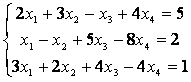 .
.
Указание
Сравните ранги матрицы системы и расширенной матрицы.
Сравним ранги матрицы системы
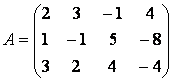
И расширенной матрицы
 .
.
Для удобства вычислений будем искать ранг матрицы А1, отделив ее последний столбец вертикальной чертой. Тогда столбцы, стоящие слева от черты, образуют матрицу А, и мы одновременно найдем ранги обеих матриц.
А1 ~ 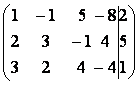 .
.
Вычтем из второй строки удвоенную первую, а из третьей – первую, умноженную на 3:
А1 ~ 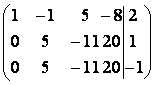 ~
~ 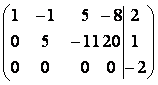 .
.
Таким образом, R(A) = 2, a R(A1) = 3, следовательно, система не имеет решений.
Ответ: система несовместна.
Задача 3.
Найти общее решение линейной системы
 .
.
Указание
Убедившись в том, что система совместна, определите базисные и свободные неизвестные и выразите базисные неизвестные через свободные.
Решение
Найдем R(A) и R(A1):


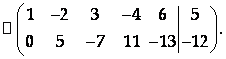
Итак, R = R(A) = R(A1) = 2, а число неизвестных П = 5. Следовательно, R < N, и система имеет бесконечно много решений (совместна, но не определена).
Число базисных неизвестных равно R, то есть двум. Выберем в качестве базисных неизвестных Х1 и Х2, коэффициенты при которых входят в базисный минор преобразованной матрицы А:  .
.
Соответственно Х3, Х4, Х5 – свободные неизвестные.
Запишем систему, равносильную исходной, коэффициентами в которой являются элементы полученной матрицы:
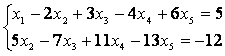
И выразим базисные неизвестные через свободные:
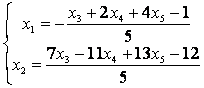 .
.
Получено общее решение системы. Одно из частных решений можно найти, положив все свободные неизвестные равными нулю: Х3 = Х4 = Х5 = 0. Тогда
![]()
Ответ: 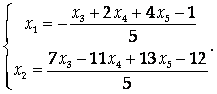
Задача 4.
Найти общее решение системы, выразив в ответе первые неизвестные через последние:

Указание
Приведите расширенную матрицу к виду

Решение

Минор, состоящий из первых трех столбцов полученной матрицы,
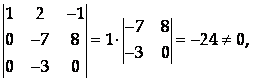
Поэтому R(A) = R(A1) = 3, выбранный минор является базисным, а Х1, Х2, Х3, коэффициенты при которых составляют базисный минор, – базисными неизвестными. Тогда свободное неизвестное – Х4, и система, равносильная исходной, имеет вид:
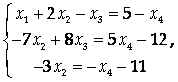
Откуда 
Ответ: ![]()
Задача 5.
Найти фундаментальную систему решений однородной линейной системы
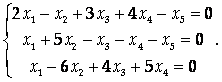
Указание
Количество решений, образующих фундаментальную систему, равно числу
Свободных неизвестных. Задайте свободным неизвестным значения 1,0,0; 0,1,0; 0,0,1 и вычислите соответствующие значения базисных неизвестных.
Решение
|
Количество решений, образующих фундаментальную систему, равно числу Свободных неизвестных. |
Матрица А1 отличается от матрицы А только добавлением нулевого столбца свободных членов, поэтому все ее ненулевые миноры являются минорами матрицы А, то есть R(A) = R(A1). Найдем R(A):
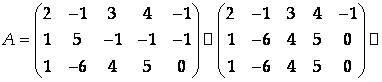
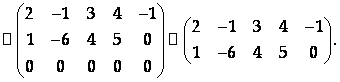
Выберем в качестве базисного минора 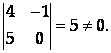
Значит, R(A) = 2. Пусть Х4, Х5 – базисные неизвестные, Х1, Х2, Х3 – свободные неизвестные. Запишем для них новую систему:
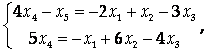
Откуда
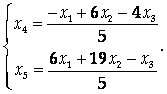
Фундаментальная система решений состоит из трех столбцов. Рассмотрим три набора значений свободных неизвестных:
1) Х1 = 1, Х2 = Х3 = 0.
Тогда Х4 = -0,2, Х5 = 1,2, и решение можно записать в виде столбца
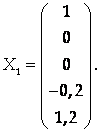
2) Х1 = 0, Х2 = 1, Х3 = 0.
При этом Х4 = 1,2, Х5 = 3,8, и следующее решение системы имеет вид
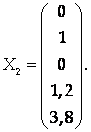
3) Х1 = Х2 = 0, Х3 = 1. Отсюда Х4 = -0,8, Х5 = -0,2, и последний столбец

|
Фундаментальная система решений, построенная при таком выборе свободных неизвестных, называется Нормальной. Поскольку столбцы свободных неизвестных |
Итак, в качестве фундаментальной системы решений можно выбрать

При этом любое решение данной системы имеет вид: Х = с1Х1 + С2Х2 + С3Х3, где С1, С2, С3 – произвольные постоянные. Эта формула задает общее решение системы.
Ответ: 
Задача 6.
Составить однородную систему из двух уравнений, для которой столбцы
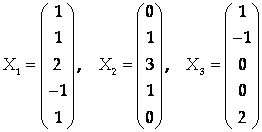
Образуют фундаментальную систему решений.
Указание
Пусть искомая система имеет вид:

Подставьте вместо Х1, …, Х5 элементы столбцов Х1, Х2, Х3 и решите полученную систему уравнений для коэффициентов Aij.
Решение
|
Существует бесконечно много систем однородных линейных уравнений, для каждой из которых фундаментальная система решений имеет указанный вид. Число уравнений в таких системах может быть различным. При этом можно указать их наименьшее требуемое количество, а увеличивать их число можно неограниченно. |
Определим вначале, из какого наименьшего числа уравнений может состоять такая система.
Число элементов каждого столбца равно пяти, следовательно, в системе пять неизвестных (П = 5). Количество столбцов, составляющих фундаментальную систему, равно трем, то есть N – R = 3, поэтому R = 5 – 3 = 2. Значит, матрица А должна иметь по крайней мере 2 строки. Следовательно, система уравнений с заданной фундаментальной системой решений может состоять из двух и более уравнений.
Пусть искомая система имеет вид:

Подставим вместо Х1, …, Х5 элементы столбцов Х1, Х2, Х3. Получим:

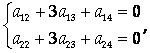

Разобьем полученные 6 уравнений на две системы, одна из которых содержит A1I, а вторая – A2I:

Найдем какое-либо частное решение этой системы. Приведем ее матрицу к треугольному виду:
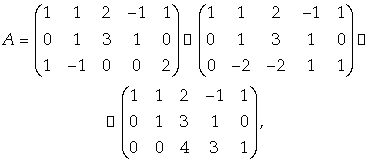
Откуда 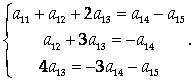
Следовательно, 
Выберем А14 = А15 = 4, тогда А11 = 0, А12 = 8, А13 = -4.
2) Так же выглядит общее решение системы для A2I:

Выберем свободные неизвестные так, чтобы получить решение, линейно независимое с предыдущим.
Пусть А24 = 4, А25 = 0, тогда А21 = 5, А22 = 5, А23 = -3.
Итак, используя найденные значения коэффициентов, можно составить линейную однородную систему:
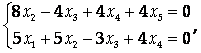
Фундаментальная система решений которой имеет вид, приведенный в условии задачи.
Ответ: 
Задача 7.
Найти общее решение неоднородной линейной системы
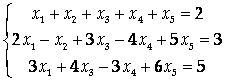
С помощью фундаментальной системы решений соответствующей однородной системы.
Указание
Убедитесь в том, что система совместна. Затем составьте соответствующую однородную систему и найдите для нее фундаментальную систему решений. Далее используйте то, что общее решение неоднородной системы линейных уравнений является суммой общего решения соответствующей однородной системы и частного решения неоднородной системы.
Решение
Убедимся в том, что система совместна:

Итак, R(A) = R(A1) = 2 – система совместна.
Составим по преобразованной матрице однородную систему:

И найдем для нее фундаментальную систему решений:

Фундаментальная система решений может быть выбрана так:
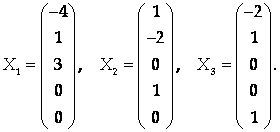
|
Общее решение неоднородной системы линейных уравнений является суммой общего решения соответствующей однородной системы и частного решения неоднородной системы. |
Теперь найдем какое-нибудь частное решение неоднородной системы

Положим Х3 = Х4 = Х5 = 0, тогда ![]() . Следовательно,
. Следовательно,
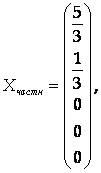 и общее решение системы имеет вид:
и общее решение системы имеет вид:
Х = с1Х1 + С2Х2 + С3Х3 + Хчастн, где С1, С2, С3 – произвольные постоянные.
Ответ: 
Задача 8.
Решить систему методом Гаусса:
 .
.
Указание
Поменяйте местами 1-е и 2-е уравнения, чтобы в первом уравнении коэффициент при Х равнялся единице, а затем исключите Х из второго и третьего уравнений.
Решение
Метод Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Для удобства его применения поменяем местами 1-е и
2-е уравнения, чтобы в первом уравнении коэффициент при Х равнялся единице:
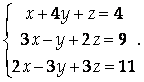
Теперь исключим Х из второго и третьего уравнений. Для этого вычтем из второго уравнения первое, умноженное на 3, а из третьего – первое, умноженное на 2:

Далее можно легко исключить Z из третьего уравнения, если прибавить к нему второе:
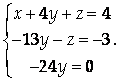
Из последнего уравнения получаем, что У = 0. Подставляя это значение в первое и второе уравнения, находим остальные неизвестные: Z = 3, Х = 1.
Ответ: Х = 1, У = 0, Z = 3.
|
При применении метода Гаусса совсем не обязательно приводить систему к «классическому» треугольному виду:
Достаточно, чтобы матрица коэффициентов, например, системы трех уравнений с тремя неизвестными содержала два нуля в одном столбце и одновременно два нуля в одной строке, причем один из нулей стоял на пересечении этих строки и столбца. |
Задача 9.
Решить систему методом Гаусса:

Указание
Исключите Х2 из 2-го и 4-го уравнений, используя 1-е уравнение, а затем вычтите из 3-го уравнения 2-е, чтобы исключить Х3.
Решение
Исключим Х2 из 2-го и 4-го уравнений. Для этого из 2-го уравнения вычтем 1-е, а к 4-му прибавим 1-е, умноженное на 2:
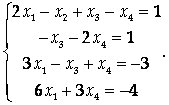
Вычтем из 3-го уравнения 2-е, чтобы исключить Х3:

Теперь вычтем из 4-го уравнения удвоенное 3-е:
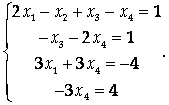
Из последнего уравнения находим ![]() . Тогда из 3-го уравнения Х1 = 0, из 2-го
. Тогда из 3-го уравнения Х1 = 0, из 2-го ![]() , из 1-го Х2 = 2.
, из 1-го Х2 = 2.
Ответ: ![]()
| < Предыдущая | Следующая > |
|---|
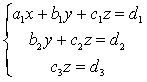 .
.