2.3.5. Метод Гаусса

При практическом решении систем линейных алгебраических уравнений удобно пользоваться Методом Гаусса, который состоит в приведении расширенной матрицы системы к ступенчатому виду. Предположим, что расширенная матрица системы (2) приведена к ступенчатому виду. Будем считать, что переменные переобозначены так, что базисный минор матрицы системы находится в левом верхнем углу:

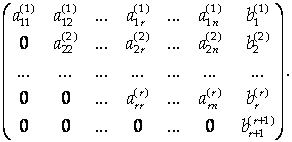
Это означает, что система (2) приведена к виду

Процесс приведения системы к виду (7) называется Прямым ходом метода Гаусса.

Если B(R+1) R+1 не равно нулю, то система несовместна. Если B(R+1) R+1 = 0, то из R-го уравнения выразим базисное неизвестное Xr через свободные неизвестные Xr+1, ..., Xn. Затем подставим это выражение в (R – 1)-ое уравнение и выразим Xr-1 через свободные неизвестные и т. д. Этот процесс называется Обратным ходом метода Гаусса. В результате обратного хода все базисные неизвестные будут выражены через свободные, т. е. будет получено общее решение системы.

Пример 2. Найдем решение системы

Методом Гаусса. Выпишем расширенную матрицу системы:

Вычтем из строк с номерами 2,3,4 и 5 первую строку, умноженную на числа 2,1,2 и 2 соответственно. Тогда получим матрицу

Вычитая из третьей и четвертой строк вторую и прибавляя к пятой строке вторую, придем к ступенчатому виду:

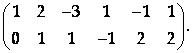
Таким образом, исходная система приведена к виду

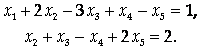
Выбрав Х1 и Х2 в качестве базисных неизвестных, с помощью обратного хода метода Гаусса находим выражения базисных неизвестных через свободные:

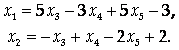
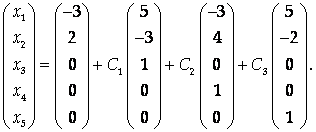
Придавая свободным переменным Х3, Х4, Х5 произвольные числовые значения С1, С2, С3, общее решение можно переписать в виде:

Упражнение 1. Найти решение системы

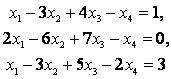
Методом Гаусса.

Решение.

Запишем расширенную матрицу системы:

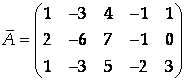
И приведем ее к ступенчатому виду. Для этого вычтем из 3-ей строки 1-ую, а из 2-ой – удвоенную первую:

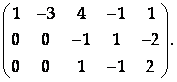
Теперь прибавим к 3-ей строке 2-ую:

Следовательно, исходная система приведена к виду

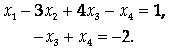
Выберем в качестве базисных неизвестных Х1 и Х3 и выразим их через свободные неизвестные Х2 и Х4:

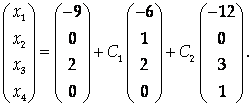
Если Х2 = С1, Х4 = С2, то общее решение системы имеет вид:

< Предыдущая		Следующая >