3.1.4. Линейные операции над векторами в координатах

1. Сложение векторов. Если А = (X1, Y1, Z1), а B = (X2, Y2, Z2), то

A + b = (X1 + X2, Y1 + Y2, Z1 + Z2). (2)

Доказательство.

Доказательство.

Имеем A = x1 i + y1 J + z1 K, B = X2 i + y2 J + z2 K. Поэтому

A + b = X1 i + y1 J + z1 K + X2 i + y2 J + z2 K = (X1 + X2) i + (Y1 + Y2) J + (Z1 + Z2) K.

2. Умножение вектора на число. Если А = (X1, Y1, Z1), то

LA = (LX1, LY1, LZ1). (3)

Доказательство.

Имеем A = X1 I + Y1 J + Z1 K. Следовательно,

LA = L(X1 i + y1 J + z1 K) = LX1 i + LY1 J + LZ1 K.

Из формул (2) и (3) вытекает, что

A – B = (X1 – X2, Y1 – Y2, Z1 – Z2).

Пример 1. Найдем координаты вектора , если А = { X1, Y1, Z1} и

В = { X2, Y2, Z2}. Имеем (см. рис. 9)

Отсюда

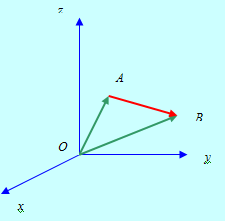
Рис. 9

< Предыдущая		Следующая >