2.2.4. Примеры решения задач по теме «Ранг матрицы»
Задача 1.
Определить ранг матрицы
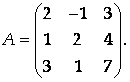
Указание
Единственным минором максимального (3-го) порядка для матрицы А является ее определитель. Если ΔА не равен нулю, R(A) = 3; если ΔА = 0, R(A) < 3.
Единственным минором максимального (3-го) порядка для матрицы А явля-ется ее определитель. Если ΔА не равен нулю, R(A) = 3; если ΔА = 0, R(A) < 3.
Найдем ΔА разложением по первой строке:

Следовательно, R(A) < 3. Поскольку матрица А содержит ненулевые элементы, R(A) > 0. Значит, R(A) = 1 или R(A) = 2. Если найдется минор 2-го порядка, не равный нулю, то R(A) = 2.
Вычислим минор из элементов, стоящих на пересечении двух первых строк и двух первых столбцов:

Ответ: R(A) = 2.
|
Если найден минор K-го порядка, не равный нулю, то можно утверждать, что R(A) ≥ K. Если же выбранный минор K-го порядка равен нулю, то из этого еще не следует, что R(A) < K, так как могут найтись миноры того же порядка, не равные нулю. |
Задача 2.
Определить ранг матрицы

Указание
Используя элементарные преобразования, приведите матрицу А к треугольному виду.
У матрицы А существуют миноры до 4-го порядка включительно, поэтому
R(A) ≤ 4. Разумеется, непосредственное вычисление всех миноров 4-го, 3-го и т. д. порядка потребовало бы слишком много времени. Поэтому, используя элементарные преобразования, приведем матрицу А к треугольному виду. Поменяем местами 1-ю и 2-ю строки, чтобы элемент А11 стал равным 1:

Прибавим к третьей строке первую, ко второй – удвоенную первую, к четвертой – первую, умноженную на 3. Тогда все элементы 1-го столбца, кроме А11, окажутся равными нулю:
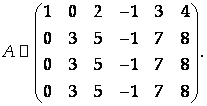
Вычтем вторую строку полученной матрицы из третьей и четвертой строк:
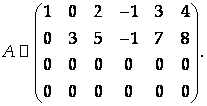
И вычеркнем нулевые строки:
 .
.
Итак, ранг матрицы А равен рангу полученной матрицы размера ![]() , т. е.
, т. е.
R(A) < 2. Минор

Следовательно, R(A) = 2.
Ответ: R(A) = 2.
Задача 3.
Определить ранг матрицы
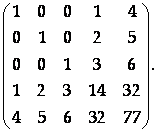
Указание
Используя элементарные преобразования, приведите матрицу А к треугольному виду.
Решение
Отметим, что минор, составленный из элементов матрицы, стоящих на пересечении первых трех строк и первых трех столбцов, не равен нулю:

Поэтому ранг данной матрицы не меньше трех.
Приведем матрицу к треугольному виду:

Вычеркивание нулевых строк приводит к тому, что

Размер полученной матрицы ![]() , поэтому ее ранг не более трех. Поскольку минор 3-го порядка, не равный нулю, существует, ранг исходной матрицы равен 3.
, поэтому ее ранг не более трех. Поскольку минор 3-го порядка, не равный нулю, существует, ранг исходной матрицы равен 3.
Ответ: R(A) = 3.
Задача 4.
Найти значения L, при которых матрица
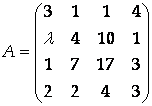
Имеет наименьший ранг.
Указание
Приведите матрицу А к треугольному виду и найдите значения L, при которых с помощью элементарных преобразований вторую строку можно сделать нулевой.
Решение
Переставим столбцы матрицы А:
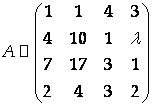
И приведем ее к треугольному виду с помощью элементарных преобразований:


Теперь видно, что при L = 0 вторая строка матрицы становится нулевой, и после ее вычеркивания получаем:

Минор 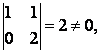 его порядок равен 2, следовательно, при L = 0 R(A) = 2.
его порядок равен 2, следовательно, при L = 0 R(A) = 2.
Если L ≠ 0, то минор, составленный из последних трех столбцов, имеет вид:

Значит, при L ≠ 0 R(A) = 3.
Итак, наименьший ранг, равный 2, матрица А имеет при L= 0.
Ответ: L = 0.
| < Предыдущая | Следующая > |
|---|