2.2.3. Приведение матрицы к ступенчатому виду

Пусть дана ненулевая матрица

Опишем алгоритм, который с помощью элементарных преобразований приводит матрицу А к некоторому более простому виду. Будем использовать только элементарные преобразования строк, чтобы в дальнейшем можно было применить тот же алгоритм к решению систем линейных алгебраических уравнений.

Найдем в матрице А ненулевой элемент Ai1J1 c минимальным номером столбца J1 и переставим I1-ую строку с первой. Тогда получим матрицу вида

Где

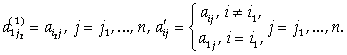
Теперь будем прибавлять к каждой строке с номером I, I = 2,...,M первую строку, умноженную на число В результате этих преобразований получим матрицу вида

Далее, с матрицей

Проведем преобразования, аналогичные тем, которые делались с исходной матрицей. Тогда исходная матрица будет приведена к виду

Продолжая этот процесс, придем к матрице Ступенчатого Вида

Для такой матрицы легко найти ранг. Действительно, выбрав первые R строк и столбцы J1, ..., Jr, получим минор

С другой стороны, любой минор порядка большего, чем R, равен нулю, так как содержит ненулевую строку. Тем самым ранг полученной матрицы равен R, а в силу того, что элементарные преобразования не меняют ранга матрицы, ранг исходной матрицы тоже равен R.

Пример 2.

Приведем к ступенчатому виду матрицу

И найдем ее ранг. Чтобы иметь дело с целыми числами, удобно иметь ненулевой элемент с минимальным номером столбца равным единице. Для этого вычтем из первой строки вторую:

Теперь будем вычитать из всех строк, начиная со второй, первую, умноженную на элемент, стоящий во втором столбце и соответствующей строке:

Вычтем из третьей строки вторую:

Вычитая из последней строки третью, приходим к ступенчатому виду:

В полученной матрице три ненулевых строки, поэтому ее ранг, а значит, и ранг исходной матрицы равен 3.

Упражнение 1.

Найти ранг матрицы

Приведя ее к ступенчатому виду.

Решение.

Поменяем местами 1-ую и 3-ю строки матрицы А:

Теперь вычтем 1-ую строку из 2-ой и 4-ой, а к 3-ей строке прибавим 1-ую, умноженную на 2:

Вычтем из 3-ей строки 2-ую, а из 4-ой – удвоенную 2-ую:

Поменяем местами 3-й и 4-й столбцы и вычтем из последней строки 3-ю:

Вычислим минор 4-го порядка из столбцов 1,2,3 и 5:

Следовательно, rg A = 4.

< Предыдущая		Следующая >