2.3.1. Решение систем линейных уравнений в общем случае

Базисным минором матрицы называется отличный от нуля минор, порядок которого равен рангу матрицы.

Пример 1. В матрице

Из примера 2 раздела «Ранг матрицы», ранг которой равен 3, базисным минором является, например, минор, получаемый при выборе строк с номерами 1,2,3 и столбцов с номерами 3,4,5. Действительно,

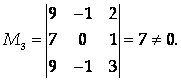
Можно выбрать и другой базисный минор, например, минор, получаемый при выборе строк с номерами 1,2,3 и столбцов с номерами 4,5,6:

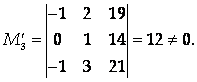
Теорема 6.1 (о базисном миноре). Любая строка (столбец) матрицы есть линейная комбинация строк (столбцов) базисного минора.

Доказательство.

В силу того, что при транспонировании матрицы базисный минор остается базисным, достаточно доказать утверждение для столбцов. Будем считать, что базисный минор порядка R находится в левом верхнем углу матрицы

(этого всегда можно добиться перестановкой строк и столбцов). Зафиксируем некоторый номер столбца K, R < K ≤ N, и рассмотрим определитель

Где 1 < I < M. Если 1 < I < R, то этот определитель равен нулю как определитель с двумя одинаковыми строками (см. следствие 2.1), а если

R < I < M, то он равен нулю как минор порядка R + 1 (ведь ранг матрицы равен R). Разложив рассматриваемый определитель по последней строке, будем иметь

Поскольку Ar+1,R+1 не равно нулю (это алгебраическое дополнение совпадает с выбранным базисным минором), то при всех 1 < I < M из равенства (1) получаем

Это и означает, что

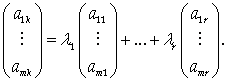
< Предыдущая		Следующая >