2.1.3. Правило Крамера

Из теоремы об обратной матрице следует, что равенство (4.3) может быть записано в виде

Следовательно,

(4)

Обозначим через ΔJ определитель матрицы, которая получается из А заменой J-го столбца на столбец свободных членов:

Разлагая этот определитель по J-му столбцу, будем иметь:

ΔJ = B1A1J + ... + BnAnj.

Тем самым равенства (4) могут быть записаны в виде

(5)

Таким образом, доказана

Теорема 4.1 (правило Крамера). Решение системы

Ax = B

С невырожденной квадратной матрицей А единственно и имеет вид (5).

Пример 2.

Найти решение системы

С помощью правила Крамера.

Имеем

Следовательно,

Упражнение 2.

Найти решение системы

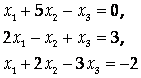
С помощью правила Крамера.

Решение.

Следовательно, система совместна и определена. Воспользуемся правилом Крамера:

Следовательно,

< Предыдущая		Следующая >