2.1.4. Примеры решения задач по теме «Решение систем с помощью обратной матрицы. Правило Крамера»

Задача 1.

Решить систему по правилу Крамера:

.

Указание

Найдите главный определитель системы (поскольку он не равен нулю, система имеет единственное решение). Затем вычислите ΔХ, ΔУ и ΔZ.

Решение

Главный определитель

Следовательно, система имеет единственное решение.

Найдем ΔХ, ΔУ и ΔZ:

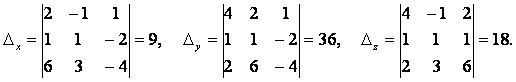
Напоминаем: определители ΔХ, ΔУ И ΔZ получены из определителя Δ заменой столбца коэффициентов при соответствующем неизвестном на столбец свободных членов.

Отсюда

Ответ: Х = 1, У = 4, Z = 2.

Задача 2.

Используя правило Крамера, выяснить, при каких значениях А система

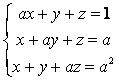
Имеет бесконечно много решений.

Указание

Для того, чтобы система была совместна, но не определена, должно выполняться условие

Решение

Главный определитель

Разложением по первой строке получим:

Следовательно, Δ = 0 при А = 1 или А = -2.

Значит, при А ≠ 1 и при А ≠ -2 система имеет единственное решение.

Определим число решений при А = 1 и А = -2.

1) При А = 1 система имеет вид:

Очевидно, что при этом система имеет бесконечно много решений, так как она фактически состоит из одного уравнения, и ее решениями будут любые три числа, сумма которых равна 1.

2) При А = -2 получаем систему

Для которой

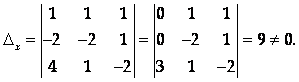
Следовательно, этом случае решений нет.

Ответ: А = 1.

Задача 3.

Решить систему с помощью обратной матрицы:

.

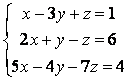Указание

Убедитесь, что матрица системы невырождена, то есть ее определитель не равен нулю. Затем найдите для нее обратную матрицу и умножьте эту матрицу на столбец свободных членов.

Решение

Составим матрицу системы:

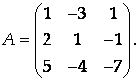
ΔА = -51 ≠ 0, следовательно, система имеет единственное решение.

Найдем матрицу А-1:

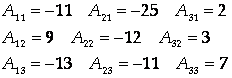
Тогда

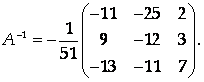
Если

То исходная система превращается в матричное уравнение АХ = В, решение которого Х = А-1В. Следовательно,

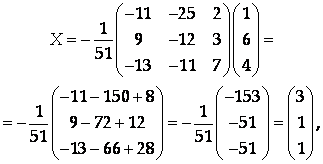
То есть Х = 3, У = 1, Z = 1.

Ответ: Х = 3, У = 1, Z = 1.

Задача 4.

Решить систему по правилу Крамера и с помощью обратной матрицы:

Указание

Для решения по правилу Крамера найдите определители D, DX, DY, DZ.

Для решения с помощью обратной матрицы составьте матрицу, обратную к матрице системы, и умножьте ее на столбец свободных членов.

Решение

1. Правило Крамера

Найдем главный определитель системы:

Система имеет единственное решение.

2. Решение с помощью обратной матрицы

Найдем алгебраические дополнения к элементам матрицы системы:

Составим матрицу, обратную к матрице системы:

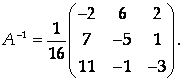
Столбец решений системы получим, умножив А-1 на столбец свободных членов:

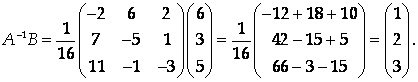
Ответ: Х = 1, У = 2, Z = 3.

< Предыдущая		Следующая >