2.1.2. Решение с помощью обратной матрицы
Пусть дана система линейных алгебраических уравнений в матричном виде (2) с невырожденной квадратной матрицей А. В силу теоремы об обрат-ной матрице (теорема 3.3) у матрицы А существует обратная матрица А-1. Умножив равенство (4.2) слева на А-1, будем иметь
А-1Ax = A-1B.
Отсюда получаем решение системы
|
X = A-1B. (3) |
Пример 1.
Найти решение системы

С помощью обратной матрицы.
Выпишем матрицу системы

Найдем присоединенную матрицу Ã. Имеем:

Следовательно,

Вычислим определитель матрицы А с помощью разложения по первой строке:
|A| = 1·(-3) + 2·(-3) + (-1)·3 = -12.
Таким образом,

Отсюда
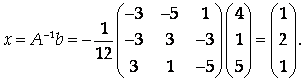
Тем самым Х1 = 1, Х2 = 2, Х3 = 1.
Упражнение 1.
Найти решение системы

С помощью обратной матрицы.
Решение.

Вычислим |A| и алгебраические дополнения к элементам матрицы А и найдем обратную матрицу:
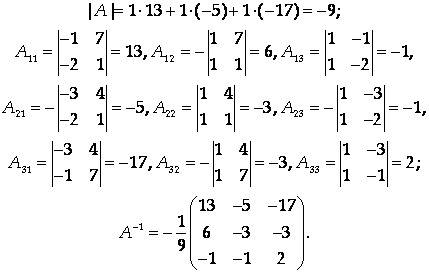
Воспользуемся формулой (3):
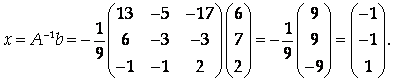
Таким образом, Х1 = Х2 = -1, Х3 = 1.
| < Предыдущая | Следующая > |
|---|