1.3.3. Обратная матрица

Пусть А – квадратная матрица порядка П. Матрица А-1 называется Обратной к матрице А, если

АА-1 = А-1А = Е.

Из того, что матрица А-1 может быть умножена на А как справа, так и слева, вытекает, что А-1 – тоже квадратная матрица порядка П.

Упражнение 1. Доказать, что (А-1)-1 = А.

Решение.

Пусть В = А-1. Тогда, поскольку по определению обратной матрицы

АВ = ВА = Е, матрица А является обратной для матрицы В, то есть

(А-1)-1 = А.

Из теоремы 3.1 следует, что |A||A-1| = |E| = 1. Таким образом, если у матрицы А существует обратная, то |A| ≠ 0 (такие матрицы называются Невырожден-ными) и

|A-1| = |A|-1.

Теорема 3.2 (о фальшивом разложении). Для любой квадратной матрицы А = ||Aij|| Порядка п справедливы равенства

Доказательство.

В случае I = J эти формулы вытекают из формул (5) темы «Определители». Докажем равенство (1) при I ≠ J. Пусть для определенности I < J. Рассмотрим определитель матрицы, которая получена из А заменой J-ой строки на I-ую. По следствию 2.1 определитель такой матрицы равен нулю. Тем не менее напишем его разложение по J-ой строке:

Остается заметить, что алгебраические дополнения Bjk совпадают с Ajk. Аналогично доказывается равенство (2) при I ≠ J (здесь вместо строк надо рассматривать столбцы и разлагать нулевой определитель по столбцу).

Для квадратной матрицы А = ||Aij|| порядка П присоединенной называется матрица

Пример 2. Найдем для матрицы

Присоединенную. Имеем

Из теоремы 3.2 непосредственно вытекает

Следствие 3.1.

Теорема 3.3 (об обратной матрице). Для любой невырожденной матрицы А обратная матрица единственна и имеет вид

Доказательство.

В силу следствия 3.1 имеем:

Тем самым матрица, определенная равенством (3.3), действительно является обратной. Докажем единственность обратной матрицы. Предположим, что нашлись две обратные матрицы А1-1 и А2-1. Тогда, умножив равенство

АА1-1 = Е

Слева на А2-1, получим:

Отсюда, в силу того, что А2-1А = Е, вытекает равенство

А1-1 = А2-1.

Пример 3. Найдем обратную матрицу для

Для нахождения присоединенной матрицы найдем сначала все алгебраические дополнения:

Следовательно (напомним, что алгебраические дополнения для элементов строк в присоединенной матрице надо расположить в соответствующем столбце),

Поскольку |A| = 1· A11 + 0· A12 + 1· A13 = - 9, получаем:

Упражнение 2. Найти обратную матрицу для

Решение.

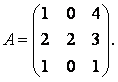
Проверим невырожденность матрицы А:

Следовательно, обратная матрица существует. Вычислим алгебраические дополнения к элементам матрицы А:

Построим присоединенную матрицу:

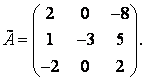
Используя теорему 3.3, находим обратную матрицу:

Упражнение 3. Доказать, что (АВ)-1 = В-1А-1.

Решение.

Пусть С = В-1А-1. Тогда, применяя свойство 1 произведения матриц, понятие единичной матрицы (лекция 1) и определение обратной матрицы, получим:

Следовательно, матрица С = В-1А-1 удовлетворяет определению обратной матрицы для матрицы АВ. Значит, (АВ)-1 = В-1А-1.

< Предыдущая		Следующая >