1.3.2. Определитель произведения матриц

Теорема 3.1 (об определителе произведения). Если А и В – квадратные матрицы, то

|AB| = |A||B|.

Доказательство.

Пусть A = ||Aij|| и B = ||Bij|| - квадратные матрицы порядка П. Из предложения 3.1

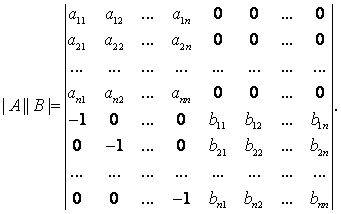
Не изменяя значения определителя матрицы, стоящего в правой части этого равенства, выполним следующие преобразования: к 1-й строке прибавим

(П + 1)-ую, умноженную на А11, (П + 2)-ую, умноженную на А12, …, (2П)-ую, умноженную на А1П. Тогда получим равенство

Где

– элементы первой строки матрицы АВ. Теперь аналогичные преобразования проведем со 2-ой строкой, т. е. прибавим к ней (П + 1)-ую, умноженную на А21, (П + 2)-ую, умноженную на А22, …, (2П)-ую, умноженную на А2П. Проведя преобразования подобного типа с остальными строками матрицы А, получим

Чтобы привести определитель матрицы, стоящей справа, к полураспавшемуся виду, поменяем местами 1-ый и (П + 1)-ый столбцы, 2-й и (П + 2)-ой, …, П – ый и (2П)-ый. Тогда

< Предыдущая		Следующая >