1.2.2. Определитель п-го порядка

Пусть дана квадратная матрица А. Минором МIj называется определитель матрицы, получаемой из матрицы А вычеркиванием I-ой строки и J-го столбца.

Пример 3. Если

То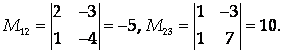

Упражнение 3. Найти М32 и М31 для матрицы

Решение.

Минор М32 получаем, вычеркнув из матрицы А 3-ю строку и 2-ой столбец:

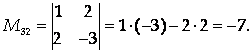
Для вычисления минора М31 вычеркиваем из матрицы А 3-ю строку и 1-ый столбец:

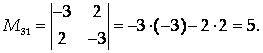
Общее понятие определителя дадим с помощью рекуррентной схемы, а именно, считая, что понятие определителя известно для матриц П–1-го порядка, дадим его для матриц П-го порядка (фактически так и вводилось понятие определителя для матриц 3-го порядка).

Определителем матрицы А = ||Aij|| Порядка п называется число

Используя знак суммы, это определение можно записать в виде:

Пример 4.

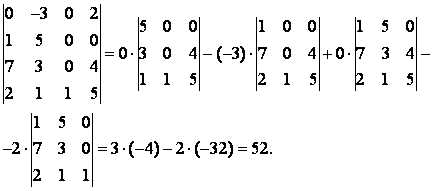
Упражнение 4. Вычислить

Решение.

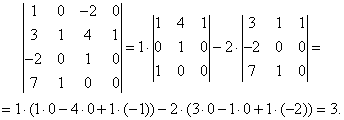
< Предыдущая		Следующая >