1.2.1. Определители матриц. Определители 2-го и 3-го порядков
Каждой квадратной матрице можно сопоставить некоторое число, называемое Определителем матрицы и обозначаемое через |A|. Прежде чем дать общее определение этого понятия, определим его для матриц 2-го и 3-го порядков.
|
Определителем матрицы 2-го порядка Называется число
|
.Пример 1.
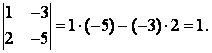
Упражнение 1. Найти определители
|
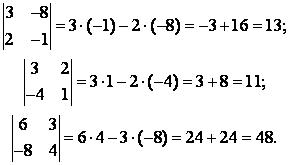
Определителем матрицы 3-го порядка называется число
|
Пример 2.
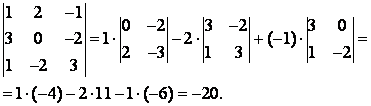
При раскрытии определителей 2-го порядка выражение для определителя 3-го порядка может быть записано в общем случае в виде
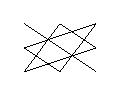Для вычисления определителя по этой формуле существует следующая геометрическая схема, называемая «правилом треугольников». Первые три слагаемых находятся перемножением элементов, стоящих на главной диагонали, и элементов, стоящих в вершинах треугольников с основаниями, параллельными главной диагонали:
Остальные три слагаемых (с минусами) получаются по аналогичной схеме:
Упражнение 2. Найти определители
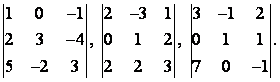
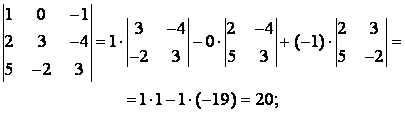
| < Предыдущая | Следующая > |
|---|
