1.1.5. Примеры решения задач по теме «Операции над матрицами»
Задача 1.
Найти матрицу 5А – 2В, если
 .
.
Указание
Используя операции умножения матрицы на число и сложения матриц, найдите сначала матрицы 5А и -2В, а затем их сумму.
Используем определения линейных операций над матрицами:
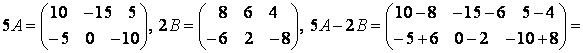
 .
.
Ответ: 5А – 2В  .
.
Задача 2.
Найти Х, У и Т, если
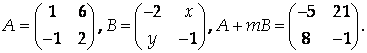
Указание
Используя операции умножения матрицы на число и сложения матриц, найдите элементы матрицы А + тВ, а затем приравняйте их соответствующим элементам матрицы ![]()
Если

 .
.
Ответ: Х = 5, У = 3, Т = 3.
Задача 3.
Найти АВ и ВА, если

Указание
Проверьте возможность перемножения матриц, определив их размерность, а затем используйте определение произведения матриц.
Решение
Проверим возможность перемножения матриц, определив их размерность.
A[![]() ], B[
], B[![]() ]. Следовательно, N = L = 4, M = K = 2, поэтому матрицы АВ и ВА существуют, причем АВ[
]. Следовательно, N = L = 4, M = K = 2, поэтому матрицы АВ и ВА существуют, причем АВ[![]() ], BA[
], BA[![]() ].
].
Для вычисления элементов матрицы С = АВ элементы строк матрицы А умножаются на соответствующие элементы столбцов матрицы В:
С11 = 2 · 2 + (-2)(-1) + 1 · 1 + 0 · 2 = 9
(сумма произведений элементов первой строки А на элементы первого столбца В; первый индекс вычисляемого элемента задает номер строки А, второй индекс – номер столбца В);
С12 = 2 · 2 + (-2) · 0 + 1 · 1 + 0 · 4 = 5;
с21 = -3 · 3 + 1 · (-1) + (-1) · 1 + 1 · 2 = -9;
с22 = -3 · 2 + 1 · 0 + (-1_ · 1 + 1 · 4 = -3.
Следовательно,

При вычислении элементов матрицы D = BA элементы строк В умножаются на элементы столбцов А:
D11 = 3 · 2 + 2 · (-3) = 0; D12 = 3 · (-2) + 2 · 1 = -4; D13 = 3 · 1 + 2 · (-1) = 1;
D14 = 3 · 0 + 2 · 1 = 2; D21 = -1 · 2 + 0 · (-3) = -2; D22 = -1 · (-2) + 0 · 1 = 2;
D23 = -1 · 1 + 0 · (-1) = -1; D24 = -1 · 0 + 0 · 1 = 0; D31 = 1 · 2 + 1 · (-3) = -1;
D32 = 1 · (-2) + 1 · 1 = -1; D33 = 1 · 1 + 1 · (-1) = 0; D34 = 1 · 0 + 1 · 1 = 1;
D41 = 2 · 2 + 4 · (-3) = -8; D42 = 2 · (-2) + 4 · 1 = 0; D43 = 2 · 1 + 4 · (-1) = -2;
D44 = 2 · 0 + 4 · 1 = 4.
Таким образом,

Ответ: 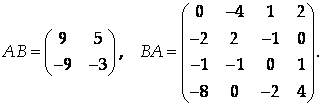
Задача 4.
Выяснить, можно ли умножить друг на друга матрицы

Если произведение существует, вычислить его.
Указание
Проверьте возможность перемножения матриц, определив их размерность, а затем (в случае, если произведение АВ или ВА существует) найдите его, используя определение произведения матриц.
Решение
Сравним размерности матриц А и В: A[![]() ], B[
], B[![]() ]. Следовательно,
]. Следовательно, ![]() поэтому произведение АВ[
поэтому произведение АВ[![]() ] существует, а произведение ВА – нет.
] существует, а произведение ВА – нет.
Найдем элементы АВ:
(Ab)11 = 0 · 5 + 3 · 7 = 21; (Ab)12 = 0 · 6 + 3 · 8 = 24; (Ab)21 = 4 · 5 – 2 · 7 = 6;
(Ab)22 = 4 · 6 – 2 · 8 = 8; (Ab)31 = 1 · 5 – 1 · 7 = -2; (Ab)32 = 1 · 6 – 1 · 8 = -2.
Ответ:  ВА не существует.
ВА не существует.
Задача 5.
Вычислить матричный многочлен А2 – 3А, где
 .
.
Указание
Найдите произведение АА и матрицу -3А, а затем сложите полученные матрицы.
Решение
Поскольку А2 = А · А, умножим матрицу А на себя по правилу умножения матриц. А – квадратная матрица 2-го порядка, поэтому А2 – тоже квадратная матрица той же размерности.
Найдем элементы матрицы С = А2:
С11 = -2·(-2) + 1 · 0 = -4;
С12 = -2·1 + 1 · 3 = 1;
С21 = 0·(-2) + 3 · 0 = 0;
С22 = 0·1 + 3 · 3 = 9.
Итак,
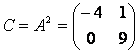 .
.
Теперь вычислим элементы матрицы D = -3A. Для этого все элементы матрицы А умножим на -3:
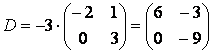 .
.
Следовательно,
 .
.
Ответ:
Задача 6.
Найти матрицу Х из уравнения Х2 = А, где

Указание
Из определения операции умножения матриц следует, что Х – квадратная матрица 2-го порядка.
Пусть

Тогда, приравнивая элементы произведения Х· Х соответствующим элементам А, получим систему уравнений для определения элементов матрицы Х.
Решение
Из определения операции умножения матриц следует, что Х – квадратная матрица 2-го порядка.
Пусть

Тогда, приравнивая элементы произведения Х· Х соответствующим элементам А, получим систему уравнений

Разделив левую и правую части второго уравнения на соответствующие части третьего, получим, что ![]() откуда B = -C. Подставим это выражение для B в систему:
откуда B = -C. Подставим это выражение для B в систему:
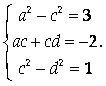
Из второго уравнения следует, что
![]()
Складывая первое и третье уравнения, найдем, что
![]()
Используя предыдущий результат, получим, что
![]()
Тогда
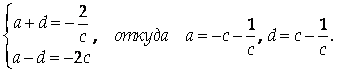
Подставим найденное выражение для D в последнее уравнение:

Вычислим остальные элементы матрицы Х:
1) если С = 1, то А = -2, B = -1, D = 0;
2) если С = -1, то А = 2, B = 1, D = 0.
Ответ: 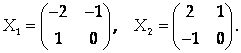
| < Предыдущая | Следующая > |
|---|