35.Многочлены от матрицы

Рассмотрим вещественную квадратную матрицу A порядка N имеющую все вещественные собственные значения. Отметим еще раз (См. параграф 1 гл.8), что .

Согласно теории Семинарских занятий 8-9 (см выше) для любой матрицы A линейного оператора φ существует невырожденная матрица T (detT ≠ 0) такая, что J = T -1AT, отсюда можно записать, что A = TJT -1. Обозначим Z+ - множество целых положительных чисел, включающее и число ноль.

Лемма 1: Для любого справедливо равенство A S = T J S T -1.

Доказательство: Доказывать будем методом мат. инд по показат. степени S.

1) - очевидно

2)

3) Пусть утв. справедливо при

4) Докажем справедливость утв. при : #

Рассмотрим жорданову нормальную форму:

, тогда Пусть жорданова клетка порядка h имеет вид :

, где , , ...,

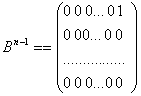, + , тогда

/здесь ЕВ=ВЕ=В по лемме о единичной матрице/==

И если Из леммы 1 вытекает.

Следствие:

Кроме того . Из формул получаем:

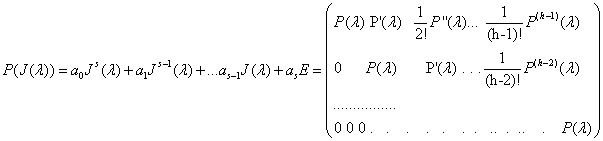
Вывод:

Элементы матрицы Однозначно определены значения многочлена Р(t) и его производных до порядка включительно в точке где - характеристическое число (с. з-ие лин. оператора ), отвечающее жордановой клетке , - размер жордановой клетки. Отсюда непосредственно следует, что из равенства не вытекает тождество , а лишь равенство

(1)

Справедливые для любого с. зн-я - max размер жорд. клетки, отвечающей

Определение 1:

Если для 2-х многочленов P(t) и Q(t) выполняются рав-ва (1), тоговорят, что мн-ны P(t) и Q(t) совпадают на спектре матр. A.

< Предыдущая		Следующая >