36.Функции от матрицы. Интерполяционный многочлен Лагранжа — Сильвестра

Определение 1:

Пусть даны ф-ия и A – вещественная кв. матр. порядка N; - все ее веществ. с. зн-я. Будем говорить, что f(t) определена на спектре матр. A, если существует набор этих чисел будем называть значениями ф-ции f(t)на спектре матр. A. Здесь - max размер жорд. Клетки, соответ. соб. зн-ю . Пусть f(t) – функция, определенная на спектре матр. A и пусть P(t) – многочлен, значения которого на спектре матр. A совпад. с соответств. Значениями функции f(t). Тогда полагаем, что f(A)=P(A).

Таким образом, ф-цию f(A) от матриц. A можно определить по следующей формуле: , где , ,

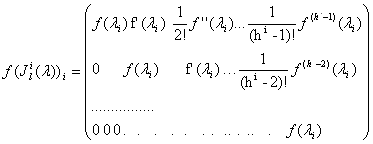
Здесь - размер жорд. клетки (индекс i – зафикс. и опущен).

Замечание 1:

Выражение для ф-ции от матр. не зависит от вида матр. T

Теорема 1 (о существовании интерполяционного многочлена Лагранжа-Сильвестра):

Пусть f(t) определена на спектре матр. A. Тогда существует единственный многочлен степени меньшей чем степень минимального многочлена матр. A И совпадающей на спектре матр. A с функцией f(t).

Доказательство: Без док-ва

Определение 2:

Многочлен из теоремы 1 наз-ся интерполяционным мн-ном Лагранжа-Сильвестра ф-ции f(t).

Вывод:

По определению ф-ции от матрицы имеем .

Замечание 2:

Из вывода следует, что ф-цию от матр. можно находить также с помощью интерполяционного многочлена Лагранжа-Сильвестра.

Теорема 2:

Пусть характеристический мн-н матр. A имеет только простые (некратные) корни. Тогда интерполяционный мн-н Лагранжа-Сильвестра имеет вид: 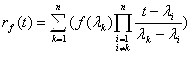, где - характерист. числа (с. зн-я) веществ. матр. A порядка N.

Доказательство: Без док-ва

Отметим, что в условии Теор.2 минимальный мн-н . Если обозначить , то формула для принимает вид:

Теорема 3:

Пусть - минимальный мн-н матр. A; - все ее характеристические числа. Обозначим 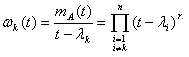. Если функция f(t) определена на спектре матр. A, то интерполяционный многочлен Лагр.-Сильвестра имеет вид:

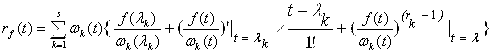
Доказательство: Без док-ва

Замечание 3:

В последней формуле выражение в фигурн. скобках – сумма первых членов разложения ф-ции по формуле Тейлора в окрестностях .

< Предыдущая