34.Теорема Жордана. Построение жорданова базиса

Пусть - линейный оператор, - все его собственные значения с кратностями равными соответственно , - соответствующие корневые подпространства, - индуцированнный нильпотентный оператор Ai на инвариантном корневом подпространстве Ri.

Определение 6: Жордановым базисом пространства V для оператора *** называется объединение жордановых базисов корневых подпространств Ri построенных для Ai.

Имеем: , где .

Фиксируем циклическое подпространство и рассмотрим индуцированный линейный оператор на инвариантном подпространстве Z. Так как , то φ(Z) < Z - инварантное подпространство. Найдем матрицу оператора в циклическом базисе Z: 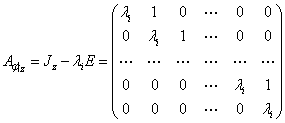, это квадратичная матрица, ее порядок равен dim Z = H. Эта матрица называется жордановой клеткой порядка H для собственного значения λI. Если , то эту матрицу обозначим . Размер жордановой клетки . Так как , то матрица A линейного оператора φ в базисе подпространства Ri имеет вид: , тогда матрица линейного оператора φ в жордановом базисе V имет вид: (5).

Таким образом, доказано следующее утверждение.

Утверждение 2: матрица линейного оператора в жордановом базисе – клеточно-диагональная. На ее диагонали располагаются жордановы клетки размеров, равных размерам циклических подпространств, на которые распадаются корневые подпространства соответствующие собственным значениям оператора φ.

Определение 7: матрицу вида (5), описанную в Утверждении 2 называют жордановой матрицей. Нахождение матрицы линейного оператора φ в его жордановом базисе назвается приведением матрицы оператора φ к жордановой нормальной форме.

Теорема 3 (Жордана):

Для любого линейного оператора , имеющего собственные значения с кратностями существует базис, в котором матрица Aφ имеет жорданову нормальную формулу J. При этом жорданова нормальная форма J однозначно определена для оператора φ с точностью до порядка расположения диагональных клеток.

Доказательство: возьмем жорданов базис в пространстве V. По Утверждению 2 матрица Aφ оператора φ имеет в этом базисе жорданову нормальную форму. Докажем единственность J.Для построения J нужны корни характеристического уравнения с кратностями . Кроме того нужны размерности циклических подпространств. Характеристический многочлен - инвариант. Размерности циклических подпространств по Теореме 2 определяются однозначно. Следовательно J – единственно (с точностью до порядка расположения диагональных клеток). #

Построение жорданова базиса и жордановой нормальной формы J линейного оператора φ, заданного матрицей A.

1) находим корни характеристического ур-я и их кратности.

2) Для каждого составляем матрицу и вычисляем rang, если rang>, товычисляем , и т. д., пока не найдется минимальная степень такая, что rang=.

3) Рассмотрим столбцы, в которых расположен базисный минор матрицы . Их линейная оболочка очевидно есть Im. Найдем подпространство =Im∩Ker. В находим базис – это те с. в-ры, с которых начинаются жордановы цепочки максимальной длины, равной , если общее число в-в в этих цепочках равно , по процесс прекращается. Если же длина цепочек <, то рассматриваем = Im∩Ker и дополняем уже выбранные векторы (из ) до базиса . Вновь добавленные с. в-ры служат началом жорданновых цепочек максимальной длины . Если общая длина цепочек <, то продолжаем построение новых с. в-ор из (дадут цепочки длиной ). И так далее, пока общая длина цепочек не окажется равной .

4) Жорданов базис получается при объединении жордановых базисов корневых подпространств.

5) Жорданова нормальная форма J матрицы A имеет клеточно-диагональный вид и может быть выписана непосредственно или получена по формуле , где T- матрица перехода от исходного базиса (E) к жорданову базису. В столбцах матр. T Стоят коорд. базис. в-в жорданова базиса.

Замечание:

Последовательно присоединенные к векторы находятся, как решения сист. лин. ур-ий вида: , где .

< Предыдущая		Следующая >