32.Разложение корневого подпространства в сумму циклических подпространств

К каждому собственному вектору базиса (E0) добавим присоединенные векторы тогда получим

(2)

Указанная система векторов (2) образует в корневом подпространстве R Базис. Отметим что каждая строка в (2) представляет жорданову цепочку.

Лемма 4: Система векторов (2) – л. н.з. когда собственные векторы 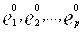- л. н.з.

Доказательство:

Доказывать будем методом математической индукции по числу векторов N в системе

1) N=1 – один с. в-ор очевидно

2) Пусть условие справедливо для (N-1) вектора системы

3) Докажем справедливость утверждения для N векторов

Пусть

Применим к данному равенству нильпотентный оператор А:

- линейная комбинация векторов (2) с числом слагаемых меньших чем (N-1) тогда в равенстве (*) остаётся

и , если -л. н.з. #

Лемма 5:

Любой вектор Представим в виде линейной комбинации системы векторов (2).

Доказательство:Пусть , m-его высота тогда Где l - показатель нильпотентности оператора А Будем доказывать методом математической индукции по высоте вектора m

1) M=1 => Или x - собственный вектор оператора А (т. е. ) по построению базиса () вектор Х разлагается по

2) Пусть утверждение справедливо для высоты m

3) Докажем справедливость утв-я для высоты ( m+1)

Пусть - произвольный вектор высоты ( m+1) рассмотрим , очевидно что А поэтому .По построению() любой вектор в подпространстве Разлагается по базисным векторам из Т. е. найдуться векторы такие что Но векторы из Имеют m присоединенных векторов и для m-ых векторов справедливо

Тогда => вектор Т. е. имеет высоту m и по предположению индукции разлагаема по базисным векторам системы (2) отсюда и вектор Х Разлагается по векторам системы (2) #

Теорема 1:

Подпространство R В котором задано нильпотентное преобразование А Разлагается в прямую сумму подпространства циклических относительно оператора А

Доказательство:

По леммам 4 и 5 строится базис R являющийся объединением циклических базисов. Линейная оболочка каждой цепочки из (2)-циклическое подпространство т. е. , где #

< Предыдущая		Следующая >