30.Нильпотентные преобразования. Свойства нильпотентных операторов
Определение 1:
Линейный оператор ![]() A (матрица А) называется нильпотентным (нильпотентной), если
A (матрица А) называется нильпотентным (нильпотентной), если ![]() такое что
такое что ![]() ( (
( (![]() =+). Здесь +-нулевая матрица; (-нулевой оператор (См. §1 Гл.1 и §2 Гл.2 соответственно).
=+). Здесь +-нулевая матрица; (-нулевой оператор (См. §1 Гл.1 и §2 Гл.2 соответственно).
Наименьшее (min) такое что: ![]() называется показателем (степенью) нильпотентности оператора (матрицы).
называется показателем (степенью) нильпотентности оператора (матрицы).
Свойства нильпотентных преобразований:
10)Все собственные значения нильпотентного оператора A равны 0.
Доказательство:
Пусть Х – собственный вектор нильпотентного оператора A , L-показатель нильпотентности, тогда ![]() =(Х=θ=
=(Х=θ=![]() И т. к. Х
И т. к. Х![]() θ, то
θ, то ![]() #
#
Следствие 1:
Если A - нильпотентный оператор, то Ker A={все собственные векторы оператора A}![]() { θ }.
{ θ }.
Доказательство:
Вытекает из определения нильпотентного оператора и свойства 1 #
20)Пусть A - нильпотентный оператор и ![]() Выполняется
Выполняется ![]() θ и
θ и ![]() = θ тогда векторы
= θ тогда векторы ![]() Л. н.з.
Л. н.з.
Доказательство:
Векторы ![]() - корневые векторы оператора A, принадлежащие одному и тому же собственному значению
- корневые векторы оператора A, принадлежащие одному и тому же собственному значению ![]() (т. к. A – нильпотентный оператор, см. Свойство
(т. к. A – нильпотентный оператор, см. Свойство ![]() ) с попарно-различными высотами k, k-1,…,2,1.
) с попарно-различными высотами k, k-1,…,2,1.
По Лемме 2 §2 настоящей главы указанные векторы являются л. н.з. #
Следствие 2:
Любой набор векторов ![]() оканчивающийся ненулевым вектором, л. н.з.
оканчивающийся ненулевым вектором, л. н.з.
Доказательство:
Указанный набор векторов является л. н.з.,как подсистема л. н.з векторов: ![]() (см. Свойство 20, K-1
(см. Свойство 20, K-1![]() ) #.
) #.
Следствие 3:
Показатель нильпотентности ![]()
Доказательство:
В противном случае если L>N(Например L=n+1) в пространстве ![]() Л. н.з. вектор
Л. н.з. вектор ![]() , чего быть не может #.
, чего быть не может #.
→ Если L- показатель нильпотентности, то минмальный многочлеен ![]() .
.
Доказательство:
1) ![]() анулирует оператор
анулирует оператор ![]() ,т. е.
,т. е.![]() ;
;
2) Пусть R < L (L - показатель нильпотентности, R – Степень минимального многочлена) и ![]() . Предположим, что
. Предположим, что ![]() анулирует нильпотентный оператор
анулирует нильпотентный оператор ![]() , тогда, с одной стороны,
, тогда, с одной стороны, ![]() Ө
Ө![]() Ө. С другой стороны
Ө. С другой стороны ![]() Ө,(т. к.
Ө,(т. к.![]() Анулирует
Анулирует ![]() ), но по свойству
), но по свойству ![]() векторы
векторы ![]() - л. н.з.
- л. н.з.![]()
![]() = θ, получили противоречие, поэтому R=L #
= θ, получили противоречие, поэтому R=L #
Определение 2:
Пусть A - нильпотентный оператор и ![]() Ө,
Ө, ![]() = Ө.
= Ө.
Линейная оболочка Z=L(![]() ) называется подпространством циклическим относительно оператора A (см. §4гл. III). Будем говорить, что циклическое подпространство z порождается элементом (вектором) X. По свойству 20 векторы
) называется подпространством циклическим относительно оператора A (см. §4гл. III). Будем говорить, что циклическое подпространство z порождается элементом (вектором) X. По свойству 20 векторы ![]() л. н.з. и образуют в циклическом подпространстве Z базис. Этот базис наз-ся циклическим базисом, порождаемым вектором X (dim Z = K).
л. н.з. и образуют в циклическом подпространстве Z базис. Этот базис наз-ся циклическим базисом, порождаемым вектором X (dim Z = K).
Лемма 1:
Пусть z –циклическое подпространство, порождаемое вектором X и dim Z = K>2. Тогда A(Z) – циклическое подпространство, порождаемое вектором Ax и dim A(Z) = K-1.
Доказательство:
Пусть ![]() – произвольный вектор в циклическом подпространстве Z.
– произвольный вектор в циклическом подпространстве Z.
Т. к. ![]() = θ, то
= θ, то
![]() .
.
По свойству ![]() векторы
векторы ![]() –л. н.з. составляют базис в подпространстве
–л. н.з. составляют базис в подпространстве ![]() (Z). Поэтому
(Z). Поэтому ![]() (Z) – циклическое подпространство, порождаемое вектором
(Z) – циклическое подпространство, порождаемое вектором ![]() X и dim
X и dim ![]() (Z) = K-1. #
(Z) = K-1. #
Следствие 4:
Циклическое подпространство Z инвариантно относительно нильпотентного оператора ![]() .
.
Доказательство:
![]() (z)=
(z)=![]() . #
. #
Следствие 5:
![]() , где
, где ![]() ={Ө} – нулевое пространство (формально
={Ө} – нулевое пространство (формально ![]() (
(![]() =Ө) ),
=Ө) ),
![]() Z=L(
Z=L(![]() ) – циклические подпространства инвариантны относительно нильпотентного опреатора
) – циклические подпространства инвариантны относительно нильпотентного опреатора ![]() .
.
Доказательство:
Применить K раз Следствие 4. #
Вывод:
Пусть ![]() все вещественные значение линейного оператора
все вещественные значение линейного оператора ![]() с кратностями
с кратностями ![]() соответственно и
соответственно и ![]() – соответствующие корневые подпространства. По теореме 2 §2 настоящей главы
– соответствующие корневые подпространства. По теореме 2 §2 настоящей главы ![]() . Возьмем (E) – базис пространтства V, состоящий из базисов корневых подпространств
. Возьмем (E) – базис пространтства V, состоящий из базисов корневых подпространств ![]() . Тогда непосредственно из определения матрицы оператора следует, что матрица лин. оператора
. Тогда непосредственно из определения матрицы оператора следует, что матрица лин. оператора ![]() в базисе (E) имеет блочно-диагональный (или клеточно диагональный) вид:
в базисе (E) имеет блочно-диагональный (или клеточно диагональный) вид:
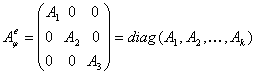
Здесь ![]() – квадратные матрицы порядков
– квадратные матрицы порядков ![]() – соответственно (по теореме 2 §2 dim
– соответственно (по теореме 2 §2 dim ![]() , причем (смотри замечание 2)
, причем (смотри замечание 2) ![]() явл-ся матрицами ограничений
явл-ся матрицами ограничений ![]() оператора
оператора ![]() на инвариантном подпространстве
на инвариантном подпространстве ![]() (по-другому индуцированного оператора
(по-другому индуцированного оператора ![]() на инвариантном подпространстве
на инвариантном подпространстве ![]() ).
).
Замечание 1:
Пусть A - нильпотентный оператор, с показателем нильпотентности K. Тогда циклическое подпространство ![]() . Рассмотрим индуцированный нильпотентный оператор
. Рассмотрим индуцированный нильпотентный оператор ![]() на инвариантном циклическом подпространстве
на инвариантном циклическом подпространстве![]() , тогда его матрица в базисе
, тогда его матрица в базисе ![]() имеет вид:
имеет вид: ![]()
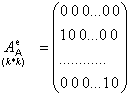
А в базисе ![]() имеет вид:
имеет вид: 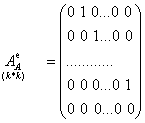
Рассмотрим лин. оператор ![]() . По Теор. 1 §2 настоящей главы корневое подпространство
. По Теор. 1 §2 настоящей главы корневое подпространство ![]() инвариантно относительно лин. оператора
инвариантно относительно лин. оператора ![]() . Введем следующий лин. оператор
. Введем следующий лин. оператор ![]() , где
, где ![]() – корневое подпространство, отвечающее
– корневое подпространство, отвечающее ![]() корню характеристич. Уравнения кратности
корню характеристич. Уравнения кратности ![]() . По определению
. По определению ![]() ,
, ![]() – нильпотентный оператор степени
– нильпотентный оператор степени ![]()
(См. Следствие 3 раздела 3.1 § 3).
Утверждение 1:
Показатель нильпотентности ![]() оператора
оператора ![]() равен кратности корня
равен кратности корня ![]() в минимальном многочлене.
в минимальном многочлене.
Доказательство:
Пусть минимальный многочлен имеет вид:
![]() .
.
Будем доказывать методом от противного. Предположим, что ![]() (
(![]() – показатель нильпотентности,
– показатель нильпотентности, ![]() – кратность
– кратность ![]() в минимальном многчлене), рассмотрим мн-н.
в минимальном многчлене), рассмотрим мн-н.
![]()
![]()
Возьмем произвольное ![]() и
и ![]() , где
, где ![]() , тогда
, тогда
![]() , т. к.если
, т. к.если ![]() , то
, то ![]()
Если же ![]() , то
, то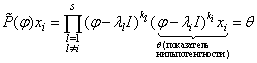
![]() (, но
(, но ![]() , отсюда
, отсюда ![]() #
#
| < Предыдущая | Следующая > |
|---|