29.Корневые векторы и корневые подпространства

Определение: Вектор X¹θ пространства V называется корневым вектором линейного оператора , если и (*).

Таким образом, в частности всякий собственный вектор является корневым (M-1). Наименьшее (min) M, при котором выполняется равенство (*) называется высотой корневого вектора Х.

Утверждения:

1) Cобственный вектор – корневой вектор высоты 1 (M=1).

2) Если справедливо , то λ - собственное значение оператора φ.

Доказательство:

Пусть Х- корневой вектор высоты M, тогда , при этом , тогда отсюда У – собственный вектор, отвечающий собственному значению λ. #

Говорят, что корневой вектор Х принадлежит собственному значению λ.

Определение: Подпространство - корневой вектор оператора φ, отвечающий собственному значению λ или X = θ} называется корневым подпространством.

Теорема 1: (о корневом подпространстве).

Корневое подпространство является подпространством пространства V.

Подпространство инвариантно относительно любого оператора , где .

Доказательство:

1) Нулевой элемент по определению

2) Если , то

3) Если и , то если , отсюда , т. е. - подпространство пространства V.

Докажем, что инвариантно относительно любого оператора , где .

Пусть , тогда , обозначим . Запишем , значит - инвариантно относительно любого оператора , кроме того #

Определение: Пусть V1 подпространство пространства V, инвариантное относительно линейного оператора φ, т. е. . В этом случае определен оператор , действующий по формуле. Линейный оператор называется ограничением оператора φ на инвариантном подпространстве V1 (по другому оператор φ индуцирует преобразование На инвариантном подпространстве V1).

Замечание:

1) Если V1 и V2 - подпространства пространства V, инвариантные относительно линейного оператора φ и , то в базисе пространства V матрица оператора φ имеет вид: , где , .

, - матрицы оператора φ, инвариантные на V1 и V2 соответственно.

2) Если же V1 - подпространство пространства V, то инвариантное относительно линейного оператора φ и других подпространств нет, то дополняя базис подпространства V1 векторами до базиса пространства V, получим матрицу оператора φ в пространстве V: , здесь *,** - ненулевые матрицы.

Лемма 1: Если , то . Иначе если и , то если (здесь λ - собственное значение оператора φ).

Доказательство:

Пусть , т. е. и

Тогда и т. к. , то #

Пусть - различные собственные значения оператора φ и , ,…, - соответствующие им корневые подпространства.

Утверждение: Сумма корневых подпространств является прямой, т. е. , если равенство справедливо тогда и только тогда когда , где .

Доказательство: Без доква

Следствие: Пусть - корневые векторы, принадлежащие попарно различным собственным значениям . Тогда векторы - л. н.з.

Доказательство:

Запишем равенство , тогда по утверждению получаем что и значит . #

Лемма 2: Пусть - корневые векторы, принадлежащие одному собственному значению λ, с попарно различными высотами (). Тогда векторы - л. н.з.

Доказательство:

Проведем доказательство методом математической индукции по K.

Рассмотрим в порядке возрастания высоты корневых векторов, т. е. пусть

1) При K=1: - верно

2) При K=2: . Пусть и . Тогда а из что и .

3) Пусть утверждение справедливо для (K-1) векторов.

4) Для K векторов.

. Пусть и .

Тогда 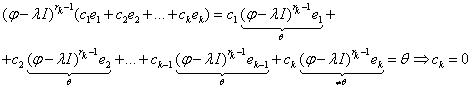, а по предположению индукции #

Теорема 2:

Пусть - собственные значения линейного оператора φ с кратностями , соответственно, а , ,…, - корневые подпространства. Тогда , ,…, и .

Доказательство:

Без доказательства.

Следствие: Максимальная высота корневого вектора, отвечающего собственному значению λ, не превосходит кратности Nλ

Доказательство: Пусть с высотой M>Nλ (доказываем методом от противного). Тогда векторы - корневые векторы, принадлежащие одному собственному значению λ с попарно различными высотами M, M-1,…, 2, 1. В самом деле, если , то корневой вектор высоты M, тогда корневой вектор высоты M-1.

- корневой вектор высоты M-2.

- корневой вектор высоты 1.

Тогда по Лемме 2 Эти векторы л. н.з. и их всего M>Nλ штук. Это противоречит тому, что #

Схемы нахождения корневых векторов.

1) Ищем собственные значения

2) Для каждого собственного значения λi решаем систему уравнений , где Ki<Ni, Ni - кратность λi как корня характеристического уравнения. Тогда находим корневые векторы максимальной высоты Ki из условия .

< Предыдущая		Следующая >