24.Приведение эрмитовой квадратичной формы к каноническому виду

Пусть – эрмитова полуторолинейная форма в унитарном пространстве, т. е. . Тогда по теоереме о представлении полуторолинейной формы существует единственный лин. оператор A, такой что .

1) Докажем, что A – самосопряженный оператор. В самом деле с одной стороны , с другой стороны , т. е. следовательно , т. е. A – самосопряж. опер.

2) Пусть - ОНБ в унитарном пространстве и - матрицы эрмитовой полуторалинейной формы и самосопряженного оператора A В унитарном пространстве. Получим связь между и .

Запишем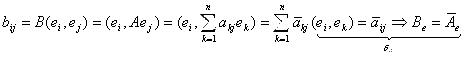

Замечание:

Если -симметричная билинейная форма в евклидовом пространстве E и , то A – самосопряженный оператор и в любой ОНБ пространства E матрицы и совпадают, т.е. .

Если в эрмитовой полуторалинейной форме положить Y=X, получим эрмитову квадратичную форму

Теорема 1:

Пусть - эрмитова квадратичная форма в унитарном пространстве U . Тогда в этом пространстве U Существует ОНБ , в котором эрмитова квадратичная форма принимает канонический вид: , где - координаты вектора X в базисе (E); - вещественные числа.

Доказательство:

Запишем: , где A – самосопряженный оператор. По спектральной теореме для самосопряж. Операторов в унитарном пространстве U существует ОНБ из собств. в-в оператора при этом

Разложим вектор X по данному ОНБ:

, тогда , отсюда

#

Теорема 2:

Пусть - квадратичная форма в евклидовом пространстве E. Тогда в этом пространстве существует ОНБ , в котором квадратичная форма принимает канонический вид:

, где - координаты вектора X в базисе (E); - собственные значения матрицы квадратичной формы.

Доказательство:

Запишем: , где A –Самосопряженный оператор. По спектральной теореме для самосопряж. Опреторов в евклидовом пространстве E Существует базис и собств. в-в оператора A, в котором его матрица, а значит и матрица квадратичной формы принимает диагональный вид, т. к. по замечанию в евклидовом пространстве в любом ОНБ. Поэтому диагональному виду оператора A соответствует канонический вид квадратичной формы . #

Вывод:

Для всякой квадратичной формы в унитарном (евклидовом) пространстве существует ортогональное преобразование, приводящее квадратичную форму к каноническому виду.

Замечание.

С каждой квадратичной формой ассоциируется самосопряженный оператор A, такой, что

Как уже отмечалось, в любом ОНБ в евклидовом пространстве матрицы квадратичной формы и самосопряженного оператора совпадаю. При приведении самосопряженного оператора A к диагональному виду одновременно с ним квадратичная форма приводится к каноническому виду, поскольку законы преобразования матрицы оператора A и матрицв квадратичной формы и совпадают, если P – ортогональное преобразование, т. е. .

< Предыдущая		Следующая >