23.Спектральная теорема для унитарных операторов и унитарных матриц

Теорема (о связи между унитарнным и нормальным оператором):

Оператор A явл-ся унитарным тогда и только тогда, когда: 1) A – нормальный оператор, 2) все собственные значения по модулю равны единице, т. е..

Доказательство:

Необходимость

Пусть A – унитарный оператор, тогда по определению следовательно , т. е. A – норм. оператор. Кроме того по св-ву 3 унитарных операторов все собст. Значения по модулю равны единице, т. е. .

Достаточность.

Пусть A – норм. опер. Тогда по спектральной теореме для норм. операторов в унитарн. простр-ве U существует ОНБ – базис из собств. в-в оператора A: . Возьмем произвольный эл-т и разложим его по данному ОНБ . Учитывая что запишем:

Если , т. е. , т. е. . Аналогично , отсюда A – унитарный оператор. #

Спектральная теорема:

1) Пусть A – унитарный оператор, действующий в унитарном пространстве . Тогда в пространстве существует ОНБ из собств. в-в оператора A, а все его собственные значения равны по модулю единице

2) Пусть - унитарная матрица. Тогда: 1) все собственные значения матрицы A равны по модулю единице, т. е. ; 2) существует унитарная матрица столбцами которой являются собственные в-ры матрицы A. такая, что

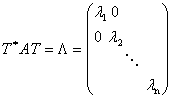
Доказательство:

Следует из предыдущей теоремы и спектральной теоермы для нормальных операторов.

< Предыдущая		Следующая >