19.Унитарный (ортогональный) оператор и его свойства

Определение:

Лин. оператор A, действующий в унитарном U (евклидовом E) пр-ве наз-ся унитарным в U (ортогон. E), если, т. е. .

Пусть - линейный оператор, здесь V=E или V=U, кроме того

Свойства:

1) .

Доказательство:

. #

Следствие: .

2) Унитарный (ортогональный) оператор переводит ОНБ снова в ОНБ.

Доказательство:

Если - ОНБ в пространстве V, то - снова ОНБ в V т. к. #

3) Собственные значения унитарного ортогонального оператора по модулю равны 1.

Доказательство (для V=U):

Пусть Al=λl, тогда #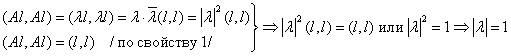

4) Пусть - произвольный ОНБ в пространстве V. Линейный оператор А является унитарным (ортогональным) тогда и только тогда, когда матрица Ae является унитарной (ортогональной).

Доказательство:

Аналогично доказательству Свойства 5 для нормальных операторов. #

< Предыдущая		Следующая >