17.Нормальный оператор и его свойства

Определение:

Лин. оператор A, действующий в унитарном U (евклидовом E) пр-ве наз-ся нормальным, если

Свойства:

Пусть A: U→ U – лин. оператор, при этом

1)

Доказательство:

#

Следствие:

2) Если А – нормальный оператор, то - также нормальный оператор

Доказательство:

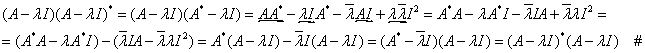
3) Если L - собственный вектор нормального оператора А, отвечающий собственному значению λ, то L - также собственный вектор оператора А*, отвечающий собственному значению .

Доказательство:

Пусть L - собственный вектор нормального оператора А, отвечающий собственному значению λ, т. е. Al=λL или . Но по Свойству 2 - нормальный оператор и по следствию из Свойства 1 справедливо , отсюда следует, что или . #

4) Собственные векторы нормального оператора А, отвечающие различным собственным значениям, ортогональны.

Доказательство:

Если , при этом по Свойству 3 .

Тогда с одной стороны , с другой стороны,

Отсюда следует, что , т. е. , т. к. #

5) Пусть - произвольный ОНБ в унитарном пространстве U. Линейный оператор А является нормальным тогда и только тогда, когда матрица Ae является нормальной.

Доказательство:

Необходимость:

Пусть А – нормальный оператор, т. е. тогда или . Но в ОНБ , отсюда - нормальная матрица.

Достаточность:

По теореме о взаимнооднозначном соответствии между множеством линейных операторов и множеством квадратных матриц можно записать: BA=AB, где , т. е оператор В имеет матрицу сопряженного оператора или . #

< Предыдущая		Следующая >